Предмет: Геометрия,
автор: XxXRifatXxX
Равнобедренный треугольник, его свойства и признаки. Урок 4
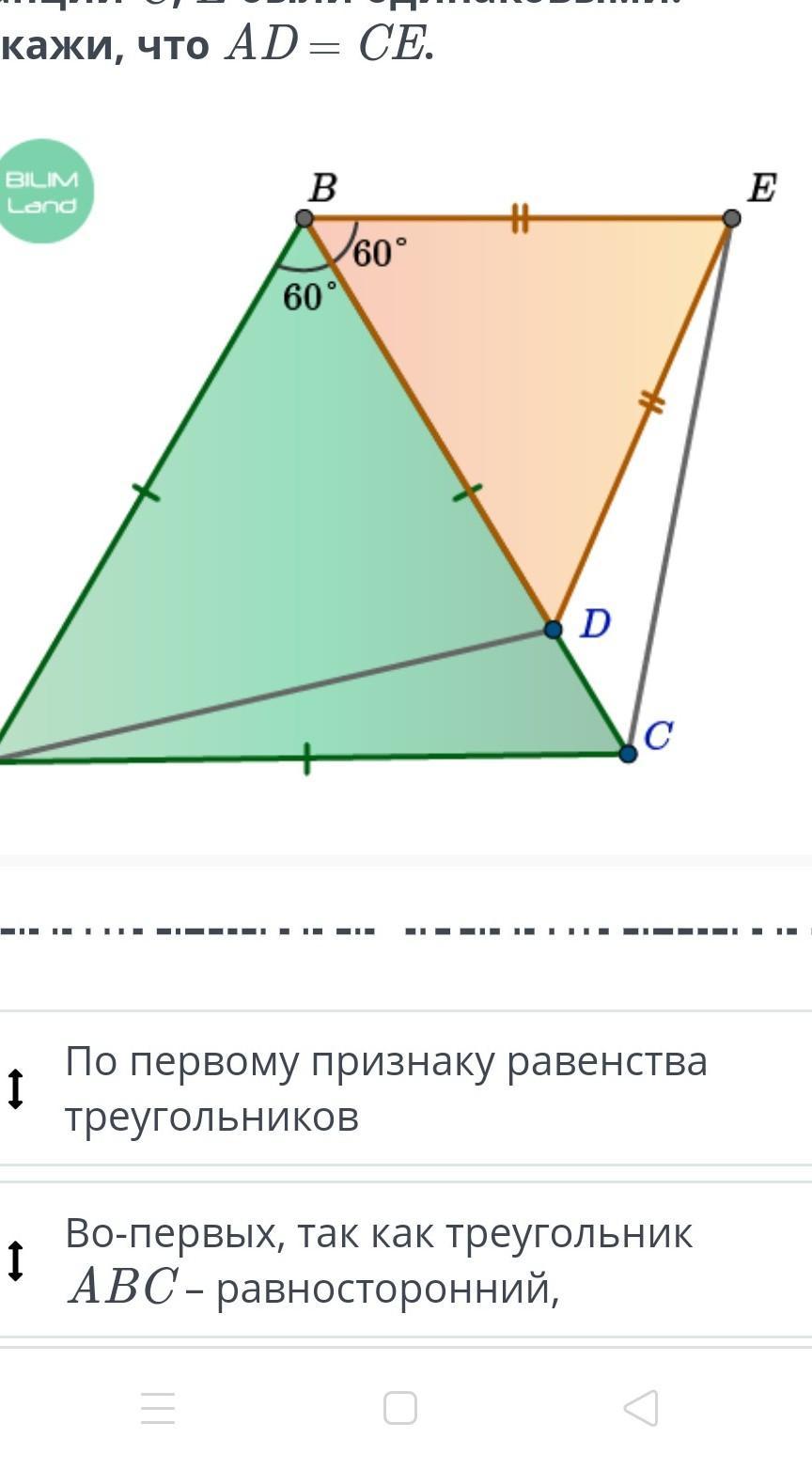
Туристическая база предлагает клиентам несколько маршрутов, проходящих через станции A, B, C, D и E. На рисунке показано расположение станций и ABC, BDE - равносторонние треугольники. Клиенты сомневаются, что длины маршрутов через станции A, D и через станции C, E были одинаковыми. Докажи, что AD = CE.
По первому признаку равенства треугольников
Во-первых, так как треугольник ABC – равносторонний,
Во-вторых, так как треугольник BDE – равносторонний,
Тогда в треугольниках ABD и CBE:
Следовательно, AD = CE.
AB = BC, BD = BE, ∠ABD = ∠DBE = 60°.
то ∠ABD = 60°.
ΔABD = ΔCBE.
то ∠DBE = 60°.
Приложения:
Ответы
Автор ответа:
1
Ответ:
Во-первых, так как треугольник ABC – равносторонний,
то ∠ABD = 60°.
Во-вторых, так как треугольник BDE – равносторонний,
то ∠DBE = 60°.
Тогда в треугольниках ABD и CBE:
AB = BC, BD = BE, ∠ABD = ∠DBE = 60°.
По первому признаку равенства треугольников
ΔABD = ΔCBE.
Следовательно, AD = CE.
Похожие вопросы
Предмет: Математика,
автор: Kris6580
Предмет: Литература,
автор: pwcalc253
Предмет: Обществознание,
автор: мелкая7
Предмет: География,
автор: Wintreist