Предмет: Алгебра,
автор: azimovashirin
помогите пожалуста, нужно с по этапным разьяснением решение
Приложения:
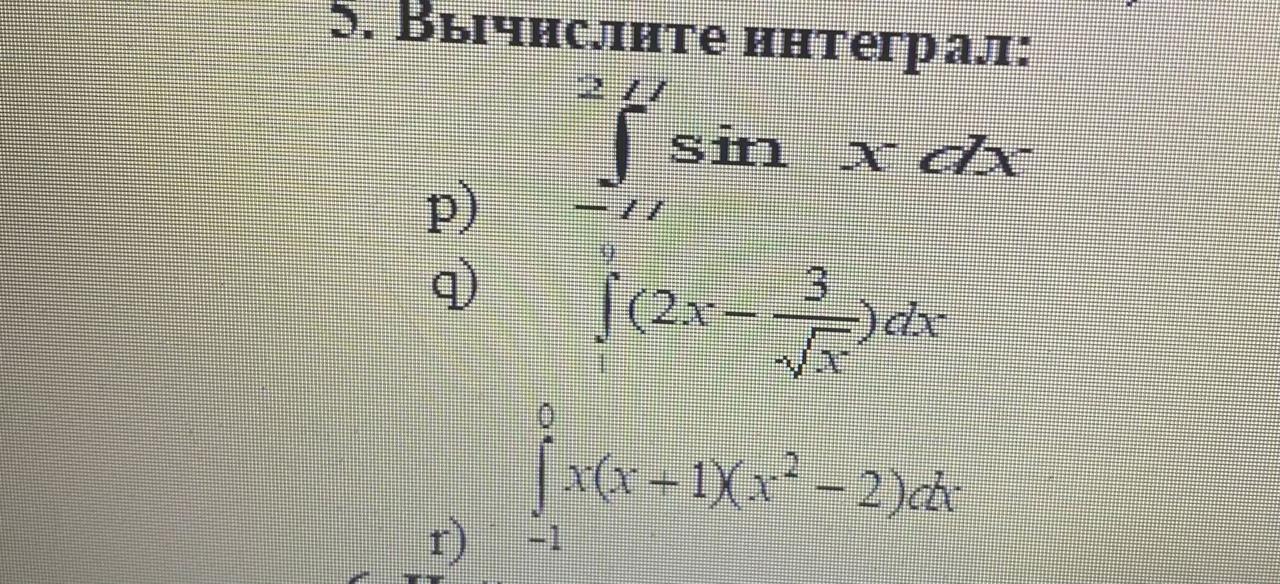
Ответы
Автор ответа:
0
Ответ:
р)
(табличный интеграл)
Подставляем пределы:
q)
Подставляем пределы:
r)
раскроем скобки
интегрируем:
подставляем пределы:
Похожие вопросы
Предмет: Литература,
автор: katka555
Предмет: Математика,
автор: 1пооо
Предмет: Химия,
автор: Ekaterina1825
Предмет: Физика,
автор: mimishka96
Предмет: Алгебра,
автор: andsavilov