Question

ПОМОГИТЕ ПОЖАЛУЙСТА!ДАМ 30 БАЛЛОВ ЗА РАЗВЕРНУТЫЙ ОТВЕТ!

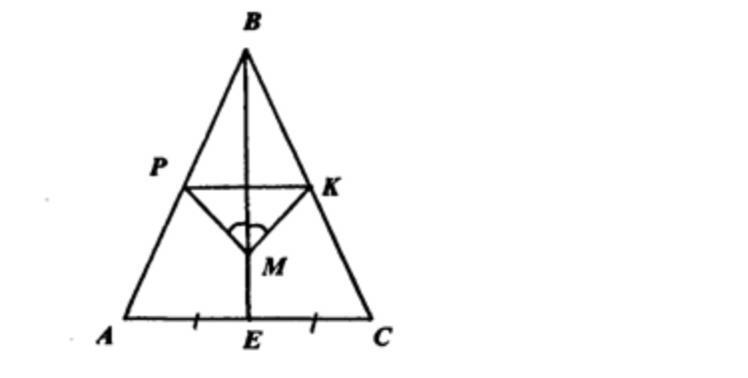
В треугольнике АВС АВ=ВЕ. На медиане ВЕ отмечена точка М, а на сторонах АВ и ВС - точки Р и К соответственно (точки Р М К не лежат на одной прямой). Известно, что угол ВМР равен углу ВМК. Докажите, что углы ВРК и ВКМ равны

Answer 1

Ответ:

$Треугольник АВС, АВ=ВС, уголА=уголС, ВЕ=медиана=высота=биссектриса, уголРВМ=уголКВМ, \: уголВМР=уголВМК, треугольник ВМР=треугольникВМК по двум углам и прилегающей стороне (ВМ-общая), значит уголВРМ=уголВКМ, ВР=ВК, треугольник РВК равнобедренный, ВН-биссектриса=высоте=медиане в треугольникеРВК, ВН перпендикулярно РК$

Answer 2

а) Т.к. ∆АВС — равнобедренный, то ВМ— биссектриса, т.о.
∠PBM = ∠MBK ⇒ ∠BPM= ∠BKM