Предмет: Алгебра,
автор: danaDel
МОЖНО С ФОТО
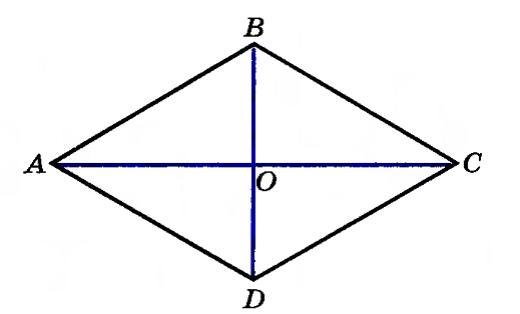
Найдите углы ромба АВСД, если его
диагонали АС =8√3 см, ВД =8.
Приложения:
iadamcuk30:
Нашол вон он
60°;120°
Ответы
Автор ответа:
1
Ответ:
60° и 120°
Объяснение:
Рассмотрим треугольник COD. Диагонали ромба перпендикулярны, следовательно это прямоугольный треугольник и ∠O = 90°, стороны треугольника OC и OD - составляют половину диагоналей, получается OC = 4√3, а OD = 4, по теореме Пифагора находим гипотенузу и получаем CD=8. По теореме косинусов выражаем угол СDO =(OD^2+CD^2-OC^2)/ 2*CD*OD = (4^2 + 8^2 - (4√3)^2)/ 2*8*4 = 0.5.
cos 0.5 = 1/2 =60°. Получается ∠CDO 60°. Диагонали ромба являются биссектрисами, следовательно ∠D=60*2=120°. Сумма углов ромба прилегающих к одной стороне равна 180°, следовательно ∠C=180-120=60°
Почему 4 в корне 3,когда дается 8 в корне.
Потому что рассматривается треугольник COD, а его катеты OC и OD - это половина диагоналей, то есть (8✓3)/2=4✓3 - OC, и 8/2=4-OD
Почему жалоба? Ответ очень подробный.
Похожие вопросы
Предмет: Математика,
автор: gggjdbk
Предмет: Русский язык,
автор: vladmansurov2
Предмет: Русский язык,
автор: traktor2004
Предмет: Математика,
автор: vilinvolk
Предмет: Математика,
автор: София2606