Предмет: Алгебра,
автор: Аноним
ПОМОГИТЕ ПОЖАЛУЙСТА!ДАМ 30 БАЛЛОВ ЗА РАЗВЕРНУТЫЙ ОТВЕТ!
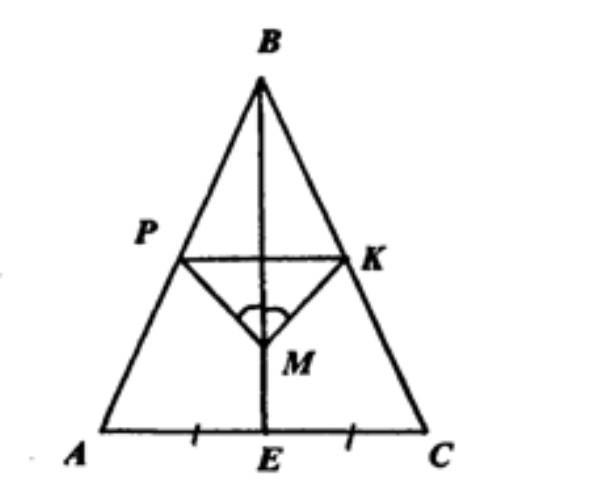
В треугольнике АВС АВ=ВЕ. На медиане ВЕ отмечена точка М, а на сторонах АВ и ВС - точки Р и К соответственно (точки Р М К не лежат на одной прямой). Известно, что угол ВМР равен углу ВМК. Докажите, что углы ВРК и ВКМ равны
please explain!
NNNLLL54:
угол BPK не равен углу BKM , но угол BPM=углу BKM , так как треугольники ВРМ и ВКМ равны по стороне (ВМ) и двум прилежащим углам ( при вершине два угла, т.к. медиана явл. и биссектрисой, и заданные по условию
Ответы
Автор ответа:
0
Объяснение:
AB=BC, следовательно ∆АВС — равнобедренный. Значит ВМ— биссектриса
∠PBM = ∠MBK ⇒ ∠BPM= ∠BKM
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: katerinayanchik
Предмет: Математика,
автор: lad2006tema
Предмет: Русский язык,
автор: horoshilovaale1
Предмет: Психология,
автор: tsyrentsydenov
Предмет: Психология,
автор: tsyrentsydenov