Предмет: Алгебра,
автор: BloodSweatTears8
Найти первую производную x y' заданных функций:
Приложения:
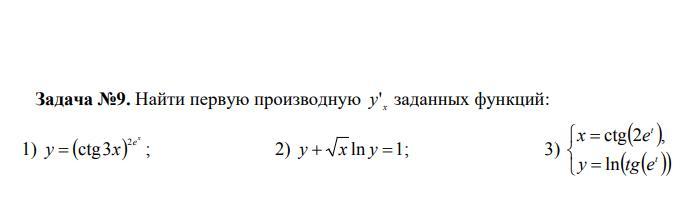
Ответы
Автор ответа:
1
Ответ:
1)
по формуле:
2)
3)
Похожие вопросы
Предмет: География,
автор: Аноним
Предмет: Математика,
автор: kamila16121982
Предмет: Математика,
автор: рфф18
Предмет: Математика,
автор: сепж298