Предмет: Математика,
автор: Ифигения
Даны: функция z=f(x,y), точка A и вектор a . Требуется найти:
1) grad z в точке A ;
2) производную в точке A по направлению вектора a ;
3) экстремум функции z=f(x,y)
Приложения:
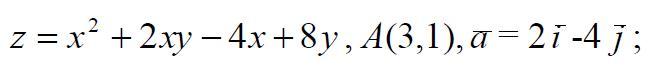

Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
z = x²+2xy-4x+8y; A(3.1); вектор а = 2i -4j
1) grad в точке А
⇒
направление градиента задается его направляющими косинусами
2) производная в точке A по направлению вектора a
3)
⇒ x=-4; y= 6
критическая точка M(-4;6)
производные второго порядка
AC -B² = -4 < 0 ⇒ глобальных экстремумов нет
Ифигения:
Большое спасибо!
пожалуйста. успехов -))))
Похожие вопросы
Предмет: Химия,
автор: LemonKill
Предмет: Русский язык,
автор: zlatadjon
Предмет: Русский язык,
автор: арина891
Предмет: Физика,
автор: Джеографик
Предмет: Литература,
автор: padre4