Предмет: Геометрия,
автор: alincik28
В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 64, а SL = 50. Найдите площадь боковой поверхности пирамиды.
Ответы
Автор ответа:
1
Объяснение:
Решение.
Стороны AB=AC=BC=6, так как треугольник ABC – равносторонний (основание правильной треугольной пирамиды). Гранями правильной треугольной пирамиды являются равнобедренные треугольники со сторонами AS=CS=BS. Тогда отрезок SL – высота треугольника ASC. Площадь боковой поверхности пирамиды равна сумме площадей трех его треугольных граней и равна
Ответ: 45.
Приложения:
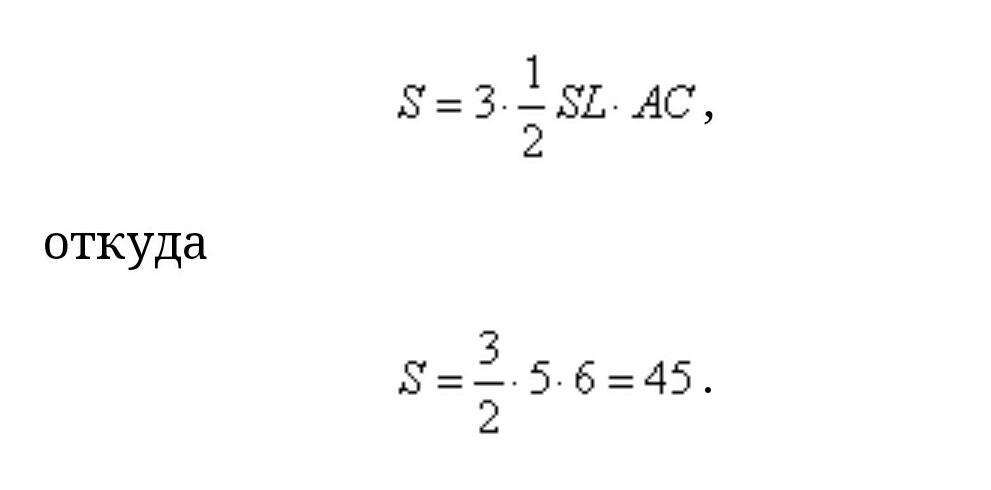
Похожие вопросы
Предмет: География,
автор: svetakovaleva15
Предмет: Физика,
автор: archegova1979
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: egpant
Предмет: Математика,
автор: NuznaPomojs