Предмет: Математика,
автор: mariamvelieva
СКАЖИТЕ ПОЖАЛУЙСТА ОТВЕТ!!!
Приложения:
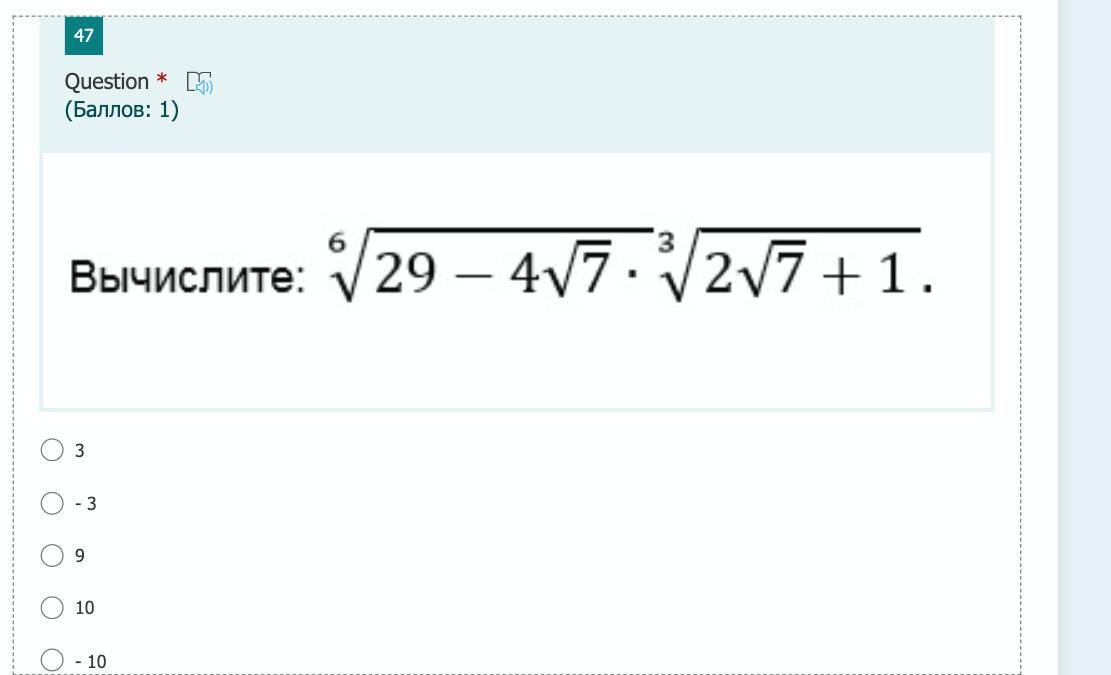


Ответы
Автор ответа:
1
Пошаговое объяснение:
Ответ: a∈(-1/3;0)U(0;+∞).
Похожие вопросы
Предмет: История,
автор: olgazaharova
Предмет: Қазақ тiлi,
автор: сашв1
Предмет: Русский язык,
автор: madinamahmudova
Предмет: Химия,
автор: nastyaabramova13