Question

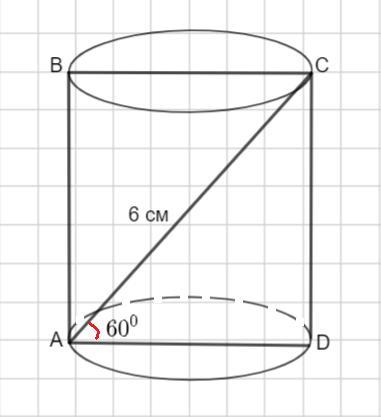
Диагональ осевого сечения цилиндра 6 см и образует с плоскостью основания цилиндра угол 60.Найти площадь полной поверхности цилиндра.​

Answer 1

Ответ:

$(9\pi \sqrt{3} +4,5\pi)$  см²

Объяснение:

Рассмотрим цилиндр. Прямоугольник ABCD- осевое сечение цилиндра

АС - диагональ осевого сечения, АС= 6 см.

∠CAD= 60°.

Площадь полной поверхности цилиндра  равна сумме площади боковой поверхности и удвоенной площади основания.

Рассмотрим треугольник Δ ACD - прямоугольный.

Если ∠CAD= 60°, то ∠ACD =90°-60°=30°.

По свойству катета лежащего напротив угла в 30°

$AD= \dfrac{1}{2} AC;$

$AD= \dfrac{1}{2} \cdot 6=3$  см

AD- диаметр окружности основания, тогда радиус основания цилиндра

R= 3 : 2=1,5 см.

Найдем CD по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$CD ^{2} =AC^{2} -AD^{2} ;\\CD = \sqrt{AC^{2} -AD^{2} } ;\\CD= \sqrt{6^{2} -3^{2} } =\sqrt{36-9} =\sqrt{27} =\sqrt{9\cdot3 } =3\sqrt{3}$

CD=H= 3√3 см.

Найдем площадь боковой поверхности по формуле:

$S= 2\pi RH;\\S=2\cdot\pi \cdot 1,5\cdot 3\sqrt{3} =9\pi \sqrt{3}$

$S=9\pi \sqrt{3}$ см² .

Площадь основания найдем по формуле площади круга

$S=\pi R^{2} ;\\S=\pi \cdot(1,5)^{2} =\pi \cdot2,25=2,25\pi$

$S=2,25\pi$ см² .

Тогда площадь полной поверхности цилиндра будет равна

$S= 9\pi \sqrt{3} +2\cdot 2,25\pi=9\pi \sqrt{3} +4,5\pi$

$S=9\pi \sqrt{3} +4,5\pi$ см²