Предмет: Математика,
автор: ejetnnet
диференциальное исчисление
Приложения:

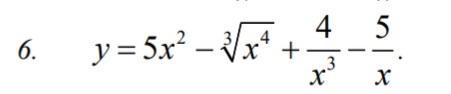
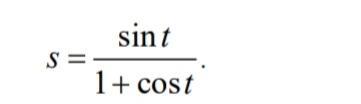
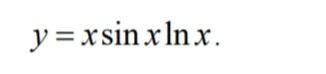
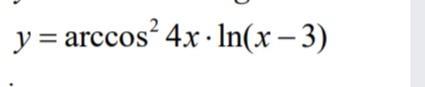
Ответы
Автор ответа:
0
Ответ:
1.
2.
3.
4.
Похожие вопросы
Предмет: Русский язык,
автор: karapetsmbatyan
Предмет: История,
автор: Klim3002bk
Предмет: Русский язык,
автор: lerusia71
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: юрец2002