Предмет: Алгебра,
автор: hol1dayy
Решите пожалуйста 
hol1dayy:
желательно через формулу двойного угла
Ответы
Автор ответа:
1
Приложения:
Автор ответа:
1
Ответ:
Объяснение:
Тут возможно прямое решение каждого из уравнений системы. Однако я для "элегантности" предложил бы следующий ход, базирующийся, на основном тригонометрическом тождестве
sin²x + cos²x = 1
Получаем, избавляясь от квадрата, из первого уравнении системы два уравнения :
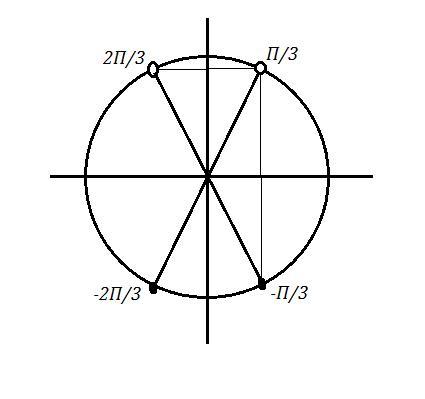
sin x = √3/2 и
sin x = - √3/2
Это можно выразить в совокупности систем уравнений (сорри, совокупности в ЛатеХе не умею рисовать):
Очевидно, первая система имеет пустое множество решений, а во второй системе решения уравнений не пересекаются:
Т.е. в ответе получаем:
Похожие вопросы
Предмет: Русский язык,
автор: jurijj809
Предмет: Химия,
автор: Skifator
Предмет: Геометрия,
автор: Mskrolik
Предмет: Математика,
автор: Участник900