Предмет: Алгебра,
автор: sonayazova
Срочно помогите . Доказать тождество
(cos^2a)2/(sin^2a)2+(cos^2a)2-1 + cos^2a/2sin^2a=0
Приложения:
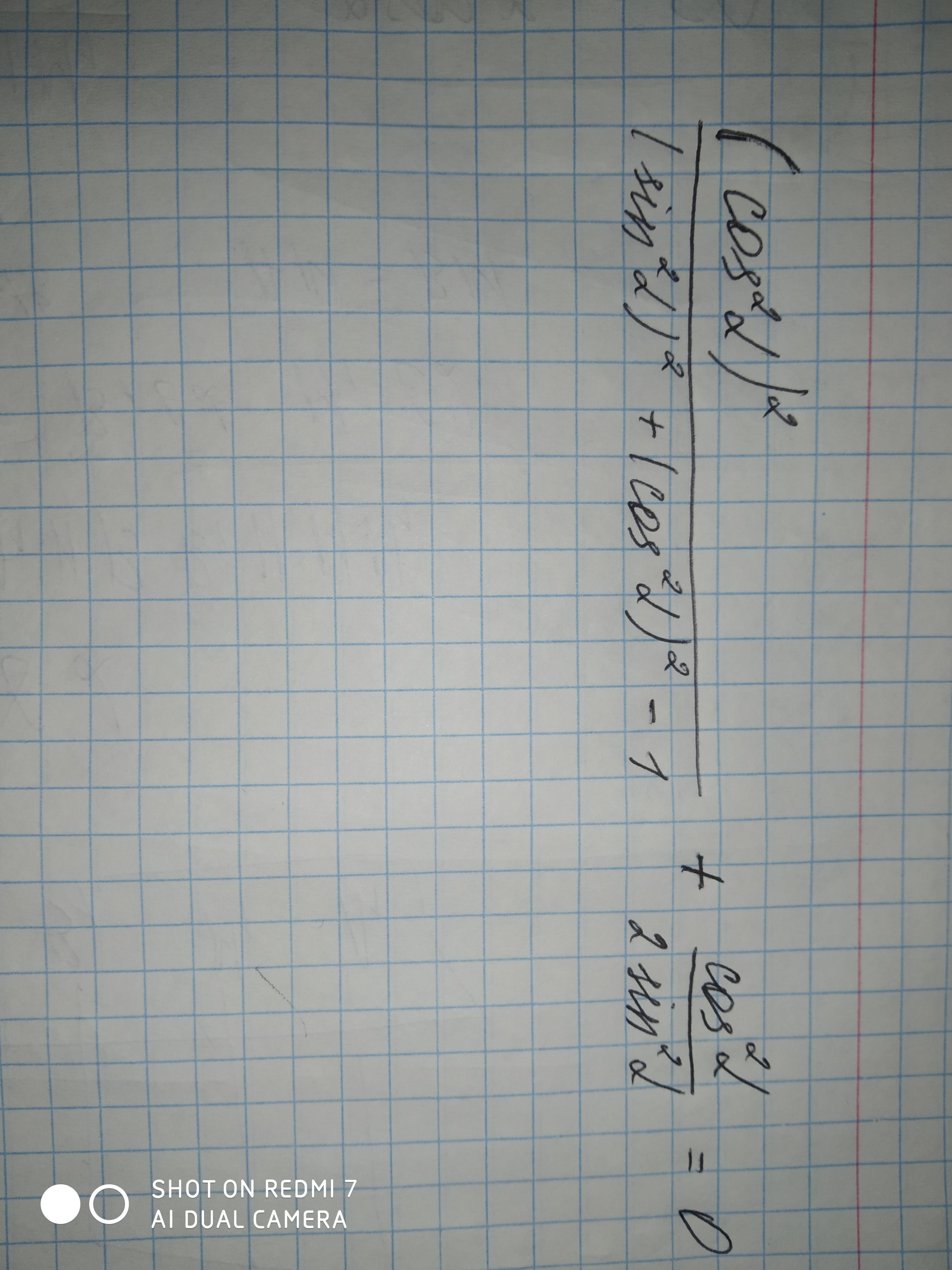
Ответы
Автор ответа:
0
Ответ:
Объяснение:
(cos²a)²/[(sin²a)²+(cos²a)²-1] + cos²a/2sin²a=0
(sin²a)²+(cos²a)²-1=(sin²a)²+(cos²a)²-sin²a-cos²a=sin²a(sin²a-1)+cos²a(cos²a-1)=
-sin²acos²a+cos²a(-sin²a)=-2sin²acos²a
Косинус в квадрате в числителе сократится с косинусом в квадрате в знаменателе. Останется косинус в квадрате в числителе деленное на -2 синуса в квадрате.
cos²a/(-2sin²a)=-cos²a/2sin²a
-cos²a/2sin²a+cos²a/2sin²a =0
Похожие вопросы
Предмет: Математика,
автор: shepotkoa
Предмет: Математика,
автор: vlf1306
Предмет: Химия,
автор: lbova1999
Предмет: Литература,
автор: Jane110509
Предмет: География,
автор: kvika1445