Question

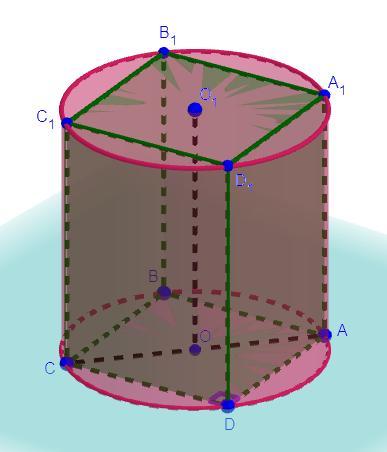
В цилиндр радиус основания которого равен5 а высота 6 вписана правильная четырехугольная призма.найдите площадь поверхности этой призмы

Answer 1

Ответ:

$\boxed{S_{p} = 20(5 + 6\sqrt{2})}$ квадратных единиц

Объяснение:

Дано: $O,O_{1} -$ центры оснований цилиндра, OA = 5, $OO_{1} = 6$, $OO_{1}$ - высота,

$ABCDA_{1}B_{1}C_{1}D_{1}$ - правильная четырехугольная призма, OA - радиус

Найти: $S_{p} - ?$

Решение: Так как по условию $ABCDA_{1}B_{1}C_{1}D_{1}$ - правильная четырехугольная призма, то определению в основании призмы лежит квадрат, следовательно $ABCD, A_{1}B_{1}C_{1}D_{1}$ - квадраты. Так как AC - диагональ квадрата ABCD и по условию OA - радиус, то точки A,O,C - лежат на одной прямой, следовательно AC - диаметр, тогда по определению AC = 2OA = 2 * 5 = 10. Так как ABCD - квадрат, то по свойствам квадрата все его углы равны 90° и все стороны равны, следовательно CD = AD = AB = CB и ∠CDA = 90°. Рассмотрим треугольник ΔCDA. Так как ∠CDA = 90°, то треугольник ΔCDA - прямоугольный, следовательно по теореме Пифагора: $CD^{2} + AD^{2} = AC^{2}$

$2CD^{2} = AC^{2}|:2$

$CD^{2} = \dfrac{AC^{2}}{2} \Longrightarrow CD = \dfrac{AC}{\sqrt{2} } = \dfrac{AC\sqrt{2} }{\sqrt{2} \cdot \sqrt{2} } = \dfrac{AC\sqrt{2} }{2} = \dfrac{10\sqrt{2} }{2 } = 5\sqrt{2}$.

По определению периметр квадрата ABCD это сумма всех его сторон, то есть $P_{ABCD} = AB + BC + CD + AD = 4CD = 4 \cdot 5\sqrt{2} = 20\sqrt{2}$.

По формуле площади боковой поверхности прямой призмы:

$S_{b} = P_{ABCD} \cdot OO_{1} = 20\sqrt{2} \cdot 6 = 120\sqrt{2}$ квадратных единиц.

Площадь основания призмы:

$S_{osn} = S_{ABCD} = CD^{2} = (5\sqrt{2})^{2} = 50$  квадратных единиц.

По формуле площади полной поверхности призмы:

$S_{p} = 2S_{osn} + S_{b} = 2 \cdot 50 + 120\sqrt{2} = 100 + 120\sqrt{2} \approx 270$ квадратных единиц.