Предмет: Алгебра,
автор: Vsvďvdheb
Очень срочно. Решите, это три номера. Заранее спасибо.
Приложения:


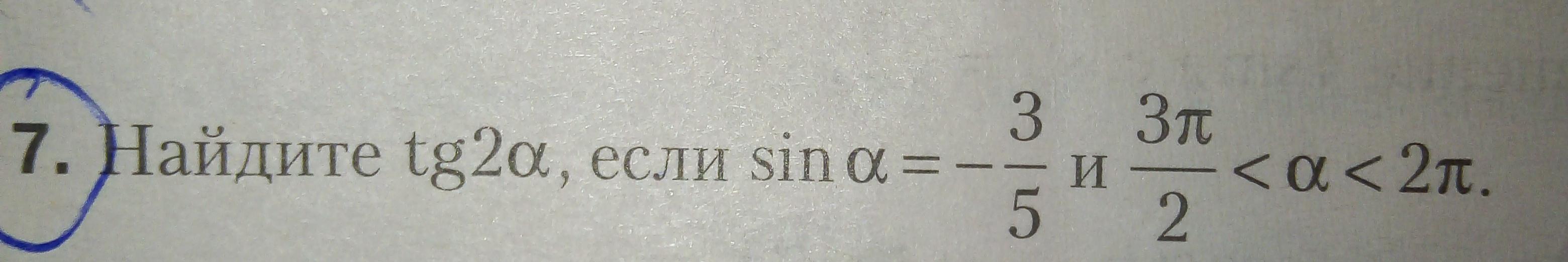
Ответы
Автор ответа:
1
8.
n принадлежит Z.
5.
угол принадлежит 3 четверти => косинус отрицательный.
7.
угол принадлежит 4 четверти => косинус положительный.
Похожие вопросы
Предмет: Математика,
автор: albinka170203
Предмет: Английский язык,
автор: Игорь059
Предмет: Русский язык,
автор: rhdhruruggy
Предмет: Физика,
автор: elizar132132
Предмет: Математика,
автор: ismailovag98p13oi4