Question

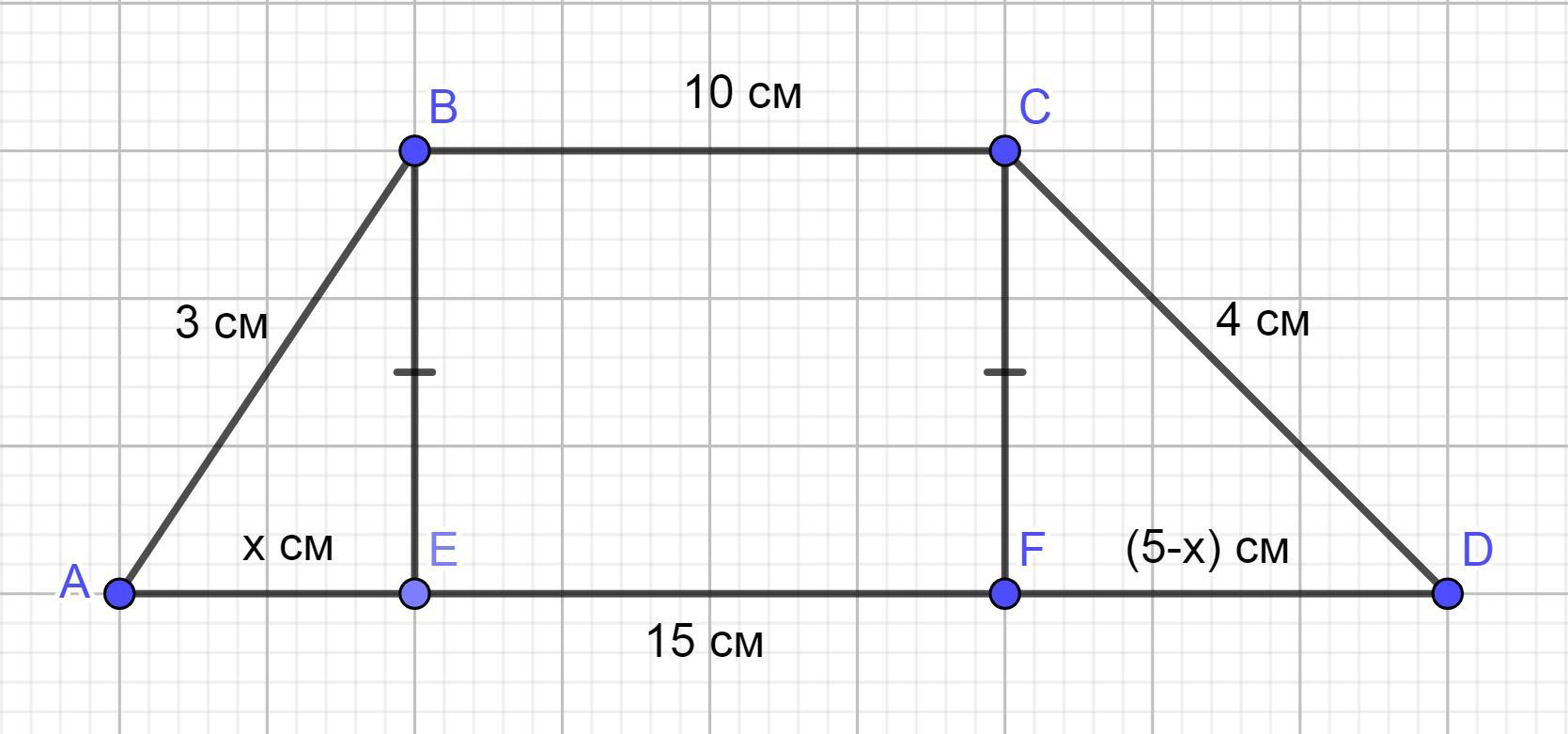
ABCD - трапеция(AD-большое основание), AB=3 см, BC=10см, CD=4 см, AD= 15 см.найдите площадь трапеции

Answer 1

Пошаговое объяснение:

Дано :

ABCD - трапеция

AD - большее основание

АВ= 3 см

ВС= 10 см

CD = 4 см

AD = 15 см

Найти :

Sтр = ? см²

Решение :

Построим трапецию ABCD . Проведем из вершины В высоту ВЕ , а из вершины С - высоту CF . По определению , BE = CF ( как высоты трапеции) . Поскольку высота -  это отрезок, перпендикулярный основанию , значит  мы получили два прямоугольных треугольника :

ΔАЕВ и ΔCFD.

Пусть  отрезок АЕ равен  х см , тогда отрезок FD будет равен :

FD = (AD - BC) - AE = ( 15- 10) - x = ( 5 - x ) см

По теореме Пифагора найдем отрезок ВЕ из ΔАЕВ :

ВЕ² = АВ² - АЕ² = 3² - x² = 9 - x²

Также , найдем отрезок CF из ΔCFD :

CF² = CD² - FD² = 4² - (5-x)² = 16 -( 25 -10x+x²) = 16 - 25 +10x -x² =

=10x - 9 - x²

Так как BE = CF , приравняем полученные значения и решим уравнение :

9 - х² = 10х - 9 - х²

9 - х²- 10х + 9 + х² =0

-10х+18=0

-10х = -18

х = -18 : (-10)

х = 1,8 см - мы нашли длину отрезка АЕ , теперь можем найти высоту ВЕ

ВЕ² = АВ² - АЕ² = 3² - x² = 9 - x² = 9 - 1,8² = 9 - 3,24 = 5,76

ВЕ = √(5,76) = 2,4 см - высота трапеции

Теперь можем найти площадь трапеции по формуле :

$\displaystyle S=\frac{a+b}{2}*h$

где a и b - основания трапеции , а h - высота

Подставим наши значения :

$\displaystyle S = \frac{10+15}{2}*2,4= 12,5 * 2,4= 30 \ cm^{2}$

Ответ : площадь трапеции ABCD равна  30 см² .