Предмет: Математика,
автор: Аноним
Мат анализ , срочно
100 баллов
Приложения:
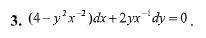
Ответы
Автор ответа:
2
Ответ:
решение на фотографии
Приложения:

Автор ответа:
2
Похожие вопросы
Предмет: Математика,
автор: alenaqwrrtyuiop1
Предмет: Русский язык,
автор: humanoid88
Предмет: Русский язык,
автор: amlikop
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: rmelnikov836