Предмет: Математика,
автор: Marginala
Найти общее решение дифференциального уравнения
Приложения:
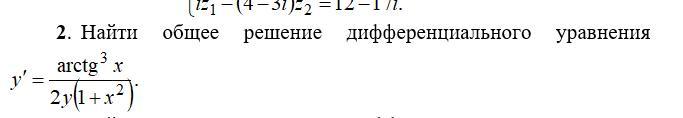
Ответы
Автор ответа:
1
Ответ:
общее решение
Похожие вопросы
Предмет: Русский язык,
автор: denis090704
Предмет: Русский язык,
автор: saidamamedova
Предмет: Другие предметы,
автор: oksanamatsievsk
Предмет: Физика,
автор: ЧумЧум
Предмет: Биология,
автор: I77Egor77I