Предмет: Геометрия,
автор: kko11ttam
а)Найдите координаты середины отрезка АВ если А (-2;3) В(6;-3)
б) Найдите длину вектора АВ
Ответы
Автор ответа:
1
Ответ:
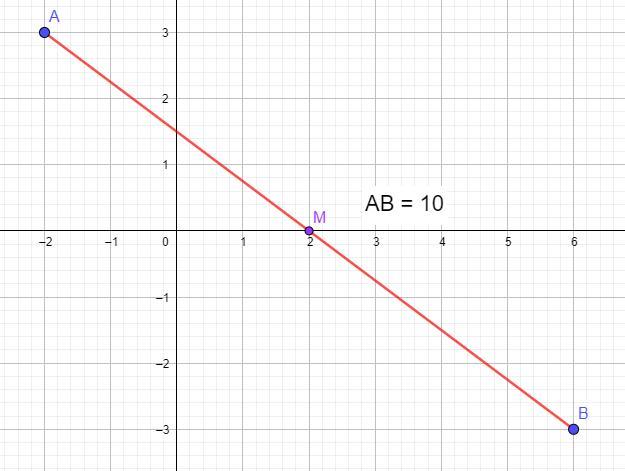
AB = 10
M(2;0)
Объяснение:
А (-2;3), В(6;-3)
Пусть M - середина отрезка AB.
По формуле координат середины отрезка:
По формуле расстояния между двумя точками:
.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: natashabaglai
Предмет: Математика,
автор: asiangirl6161
Предмет: Математика,
автор: dgjjb
Предмет: Математика,
автор: эээВасяя
Предмет: Биология,
автор: DANNY123321123