Предмет: Алгебра,
автор: sjjsjdjdjndndnd
Срочно!!! Знатоки, найдите производную графика функции y=f(x)
Приложения:
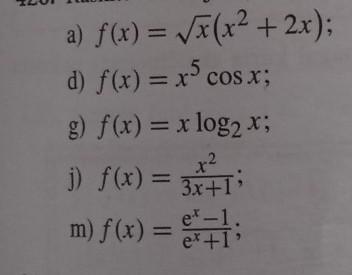
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Математика,
автор: dashagarcheva
Предмет: Математика,
автор: kok2006
Предмет: История,
автор: Laura1294
Предмет: Математика,
автор: никита3543
Предмет: История,
автор: U1HIRSAVA