Предмет: Алгебра,
автор: snotdead
Решите биквадратное уравнение, используя метод замены переменной:
Приложения:
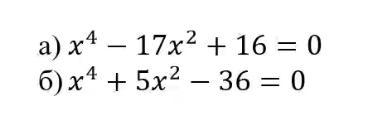
Ответы
Автор ответа:
1
а) t²-17t+16=0
D=289-4*1*16=225
t1=17+15/2=16
t2=17-15/2=1
b) t²+5t-36=0
D=25-4*1*(-36)=169
t1=-5+13/2=4
t2=-5-13/2=-9
aidana23110784:
это же не так решается :/
Неплохо, очень даже.
Автор ответа:
1
а)
Введём замену:
По теореме Виета:
Обратная замена:
Ответ: -4; -1; 1; 4
б)
Введём замену:
По теореме Виета:
Из этого случая понятно, зачем писать область значений замены рядом с ней. Если брать , то при обратной замене корней у получившегося уравнения не будет, поэтому учитывать данное значение не имеет смысла.
Обратная замена:
Ответ: -2; 2.
Похожие вопросы
Предмет: Русский язык,
автор: vap643
Предмет: География,
автор: снега1
Предмет: Физика,
автор: feridekz0083
Предмет: Алгебра,
автор: dmitriy091
Предмет: Обществознание,
автор: Libomkaor