Предмет: Математика,
автор: timchenkodima
помогите пожалуйста !!
Приложения:
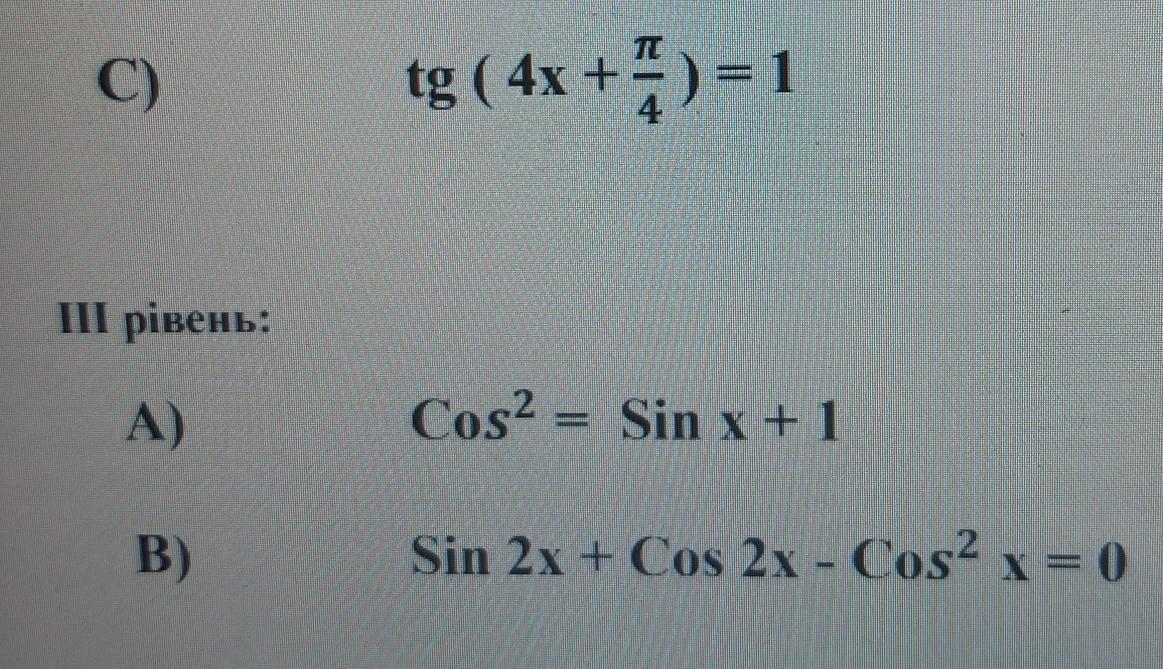
Ответы
Автор ответа:
1
C)
А)
Произведение равно нулю, когда хотя бы один из множителей равен нулю.
B)
Произведение равно нулю, когда хотя бы один из множителей равен нулю.
timchenkodima:
Спасибо огромное
Похожие вопросы
Предмет: Математика,
автор: Amop123
Предмет: Математика,
автор: maksiimmm
Предмет: Русский язык,
автор: 20kseniya04
Предмет: Экономика,
автор: vikuli4ka1998
Предмет: Литература,
автор: Аноним