Предмет: Алгебра,
автор: dashytka97
помогитеее
решить систему уравнений:
3^y*2^x+1 = 36
log (x+y) по основанию корень из 3 = 2
1 фото-уравнение
2-4-начала решать)
Приложения:
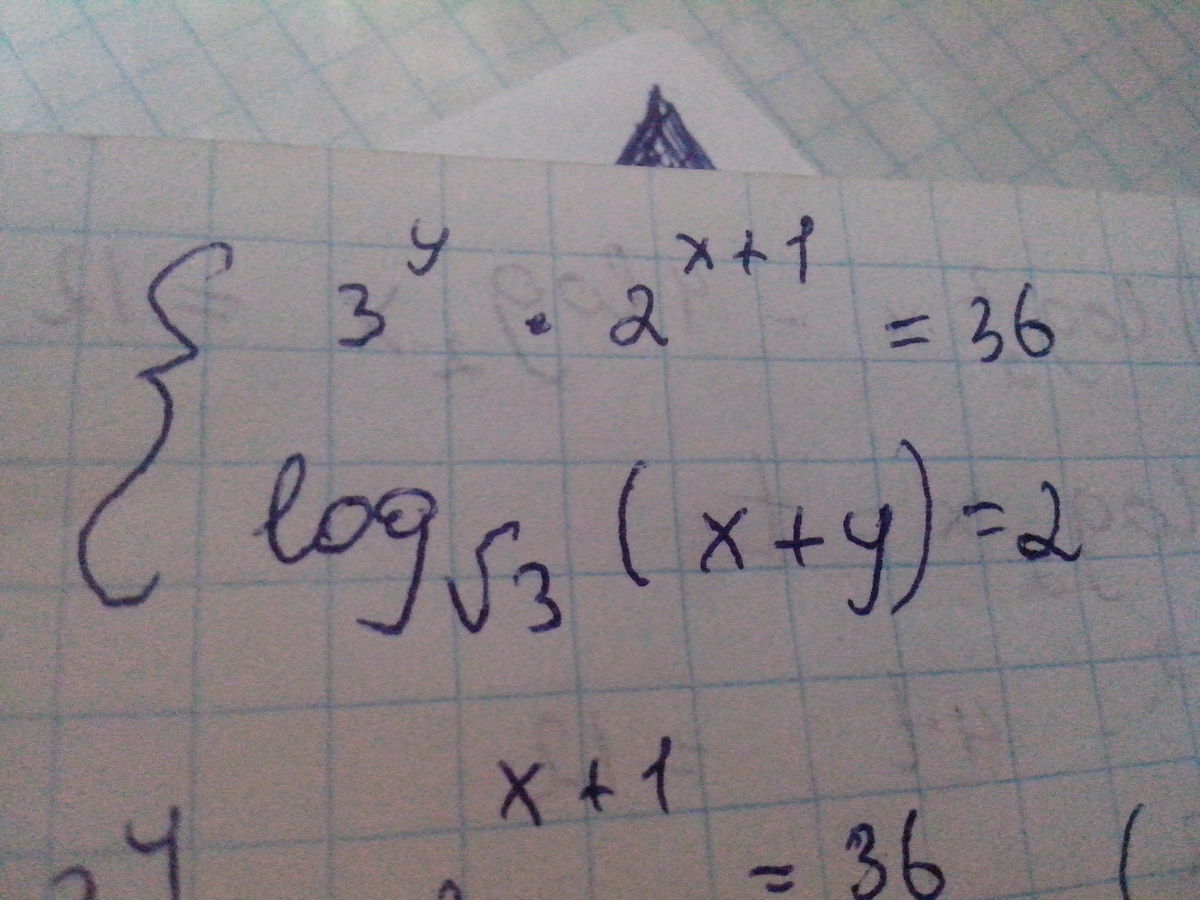
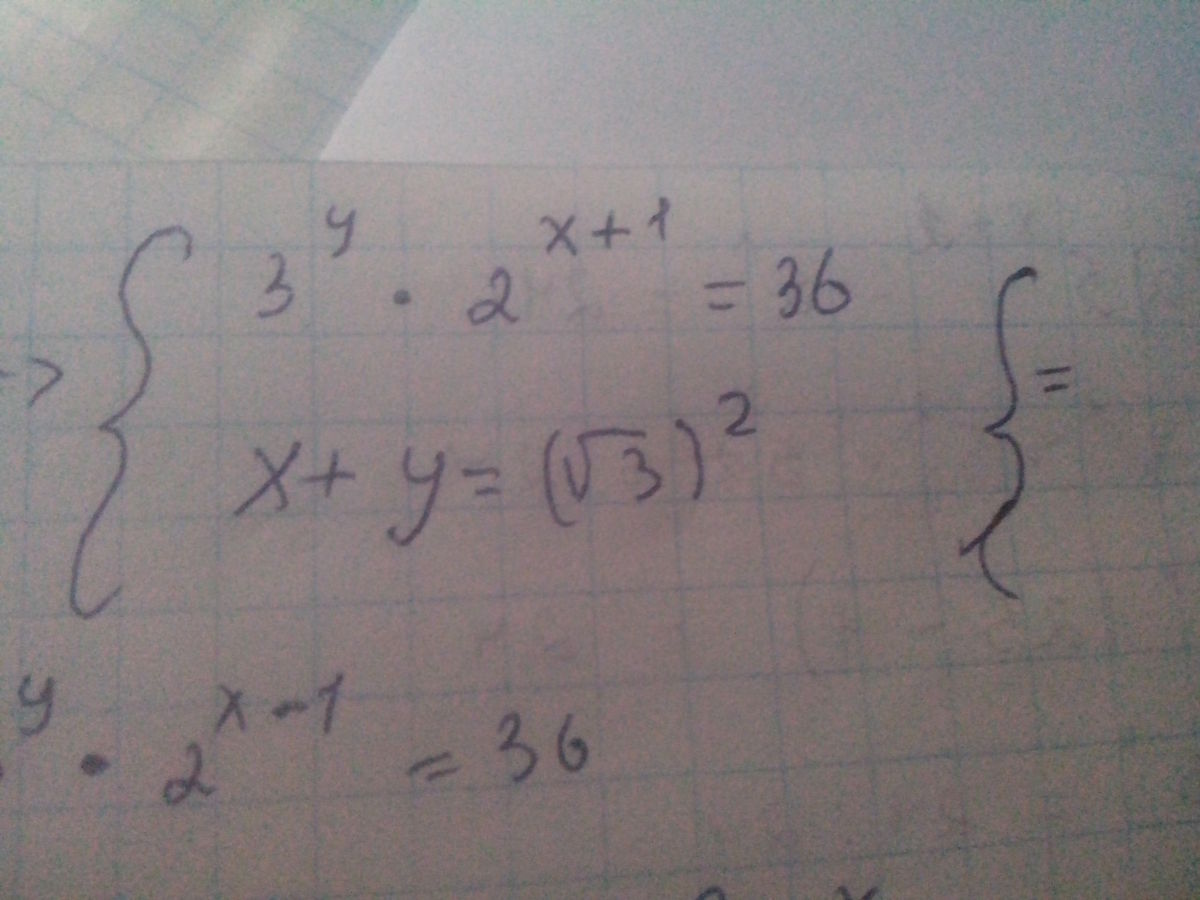
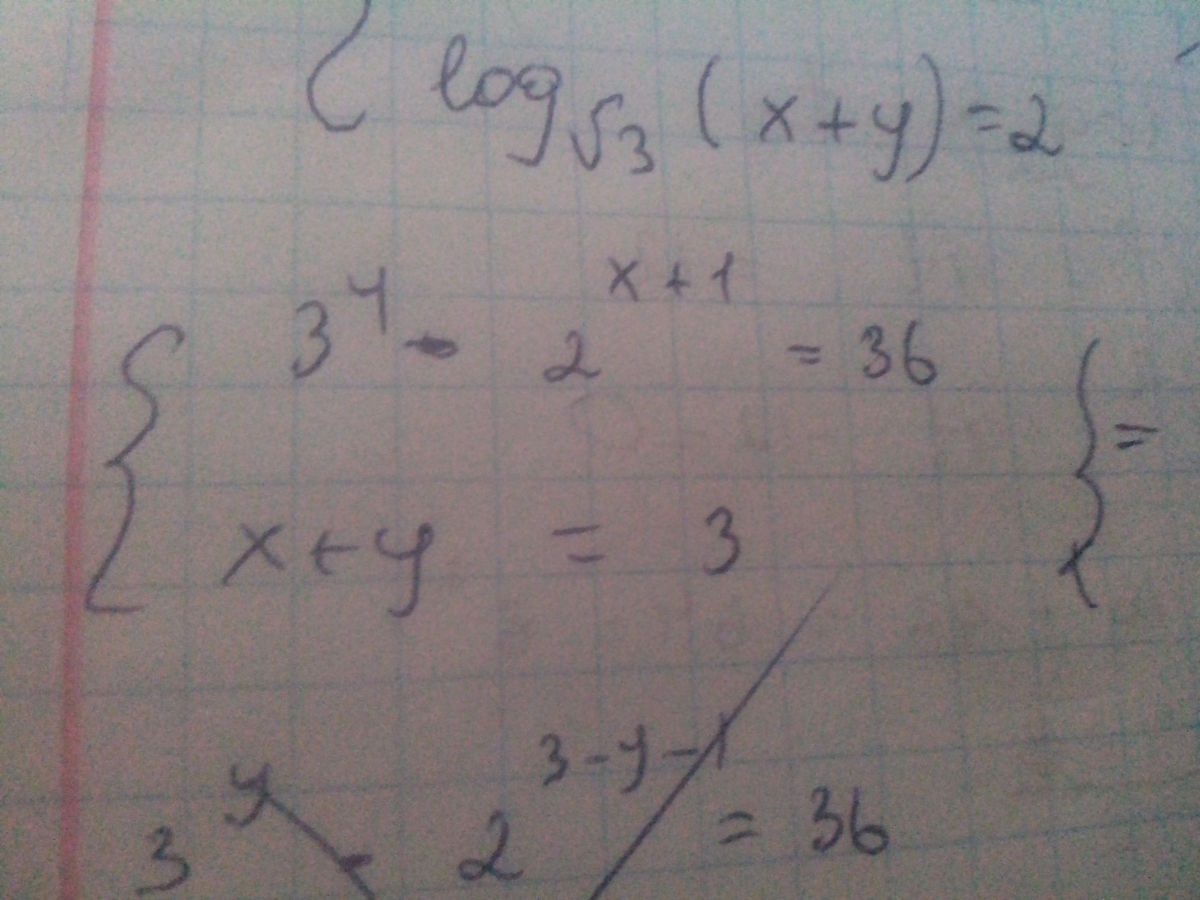
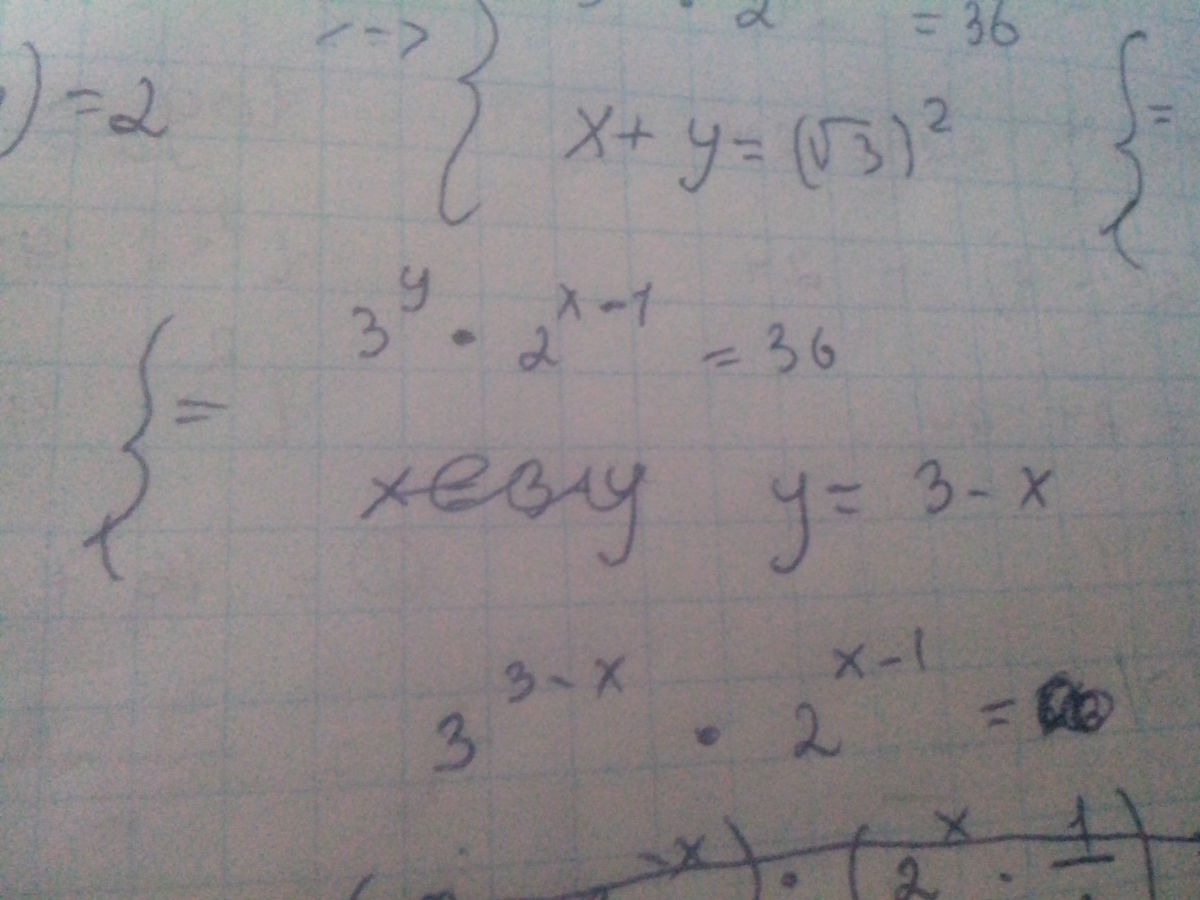
Ответы
Автор ответа:
0
{3^y*2^(x+1) = 36
{log_√3 (x+y) = 2 => x+y=(√3)^2 => x+y=3 => y=3-x
3^(3-x)*2^(x+1)=36
(27/3^x)*(2^x)*2=36
(54*2^x)/3^x=36
(54*2^x)/(1.5^x*2^x)=36
54/1.5^x=36
1.5^x=1.5
x=1
y=3-x
y=2
Проверка: 3^2*2^(1+1)=36 => 9*4=36
log_√3(1+2)=2 => log_√3(3)=2 => (√3)^2=3
{log_√3 (x+y) = 2 => x+y=(√3)^2 => x+y=3 => y=3-x
3^(3-x)*2^(x+1)=36
(27/3^x)*(2^x)*2=36
(54*2^x)/3^x=36
(54*2^x)/(1.5^x*2^x)=36
54/1.5^x=36
1.5^x=1.5
x=1
y=3-x
y=2
Проверка: 3^2*2^(1+1)=36 => 9*4=36
log_√3(1+2)=2 => log_√3(3)=2 => (√3)^2=3
Похожие вопросы
Предмет: Химия,
автор: marichaganova27
Предмет: Английский язык,
автор: egor140717
Предмет: Алгебра,
автор: qweqwewq09
Предмет: Алгебра,
автор: Daaaaashaa
Предмет: Алгебра,
автор: Зонда