Предмет: Геометрия,
автор: drogg
Помогите пожалуйста! Очень срочно
Точки E и K – середины сторон CD и AB параллелограмма ABCD,
отрезки AE и CK пересекают диагональ в точке BD
Найдите отношение BL : LP : PD
Приложения:
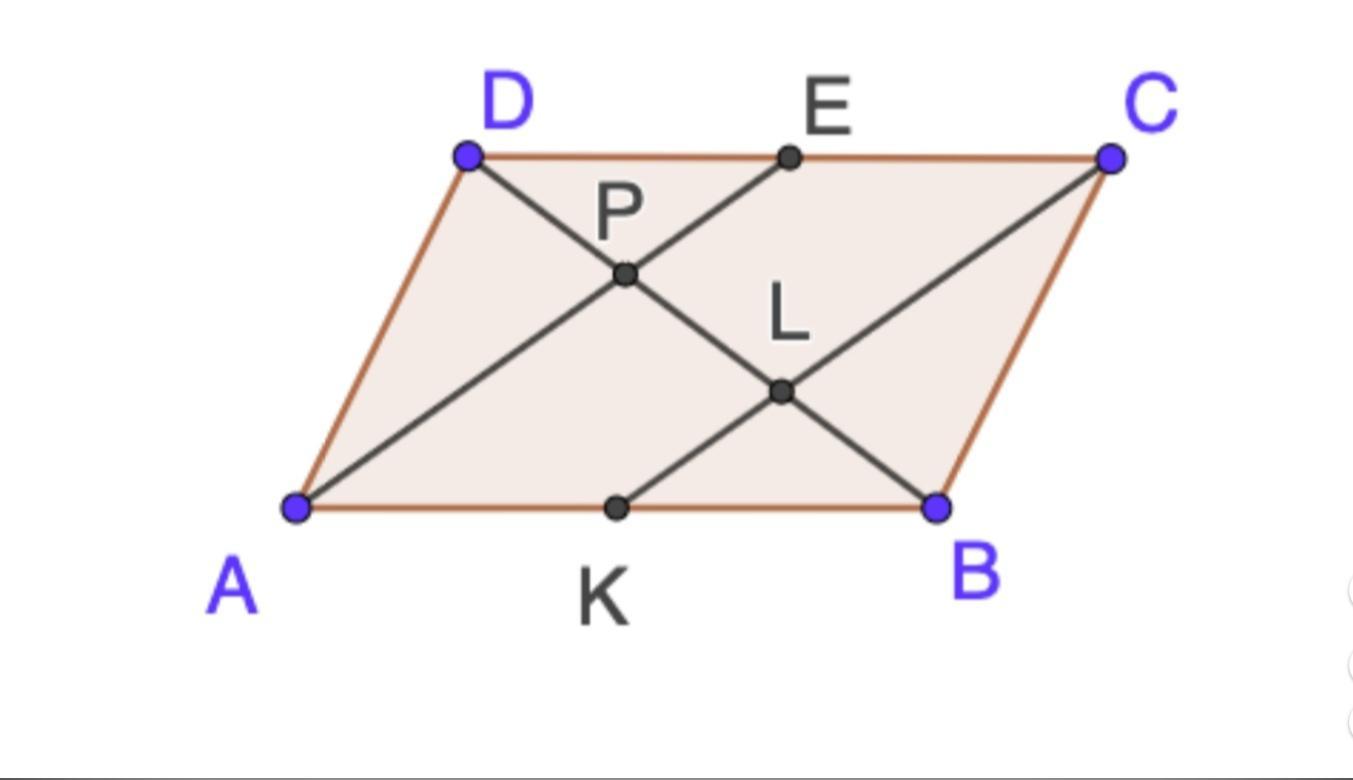
Ответы
Автор ответа:
11
АВ=CD так как противоположные стороны параллелограмма равны. Тогда 0,5*АВ=0,5*CD.
Так как К – середина АВ, то АК=0,5*АВ.
Так как Е – середина CD, то ЕС=0,5*CD.
Получим что АК=ЕС.
АК//ЕС, так как AB//CD, поскольку противоположные стороны параллелограмма параллельны.
Тогда получим что AECK – параллелограмм, так как противоположные стороны паралельны и равны. Следовательно АЕ//КС так как противоположные стороны параллелограмма параллельны.
По обобщённой теореме Фалеса: параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
То есть:
Пусть СЕ=n, тогда ED=n так же, так как CE=ED. Тогда:
Пусть AK=m, тогда КВ=m так же, так как AK=KB.
Получим что PD:LP:BL=1:1:1, или иначе говоря отрезки равны.
Ответ: 1
Похожие вопросы
Предмет: Геометрия,
автор: lyubimenikiy
Предмет: История,
автор: 1593572015gvozf
Предмет: Биология,
автор: дашулька150
Предмет: Литература,
автор: EragonLOL