Предмет: Алгебра,
автор: rabbitti
Кто сможет решить????)
Приложения:
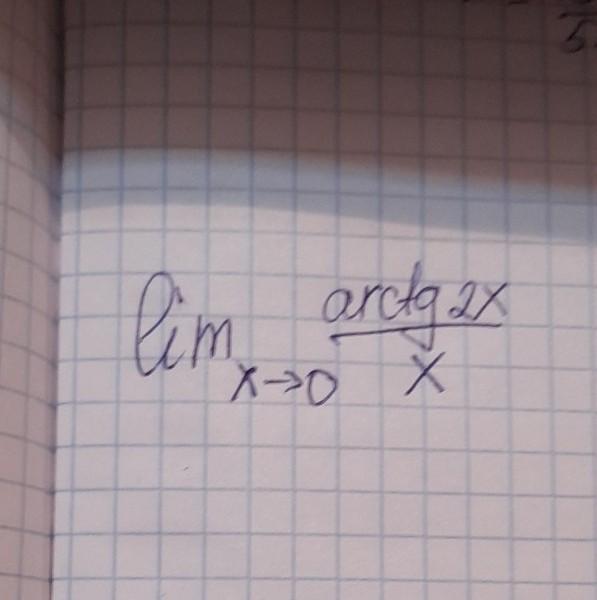
Ответы
Автор ответа:
0
Ответ:
2
Объяснение:
Применим замечательный предел:
rabbitti:
спасибооооо!!
Похожие вопросы
Предмет: Биология,
автор: nastyu555
Предмет: Математика,
автор: mmiillaann
Предмет: Русский язык,
автор: indiraametova8
Предмет: Биология,
автор: shalipov2014Ruslan