Предмет: Математика,
автор: Аноним
ПОМОГИТЕ ПОЖАЛУЙСТА
ПОСЛЕДНИЕ БАЛЛЫ ОТДАЮ
Вычисление интегралов различными способами
Приложения:
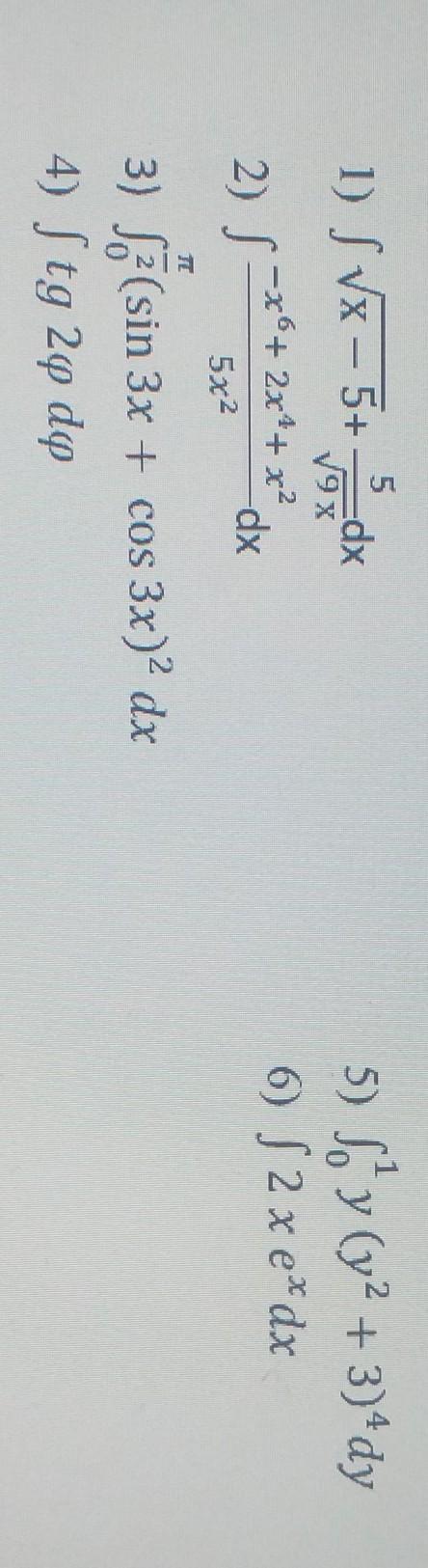
Ответы
Автор ответа:
1
Ответ:
подставляем пределы:
подставляем пределы:
по частям:
Похожие вопросы
Предмет: Русский язык,
автор: natastroitel1
Предмет: Математика,
автор: shondakova
Предмет: Математика,
автор: olegpanteleev2
Предмет: Алгебра,
автор: Dabber21
Предмет: История,
автор: 07092004m