Предмет: Математика,
автор: michaelmayers228
Нужно решить 1 дифференциальное уравнение (записать общим видом). Совсем запутался с выбором способа. Кто сможет решить, буду благодарен.

Приложения:
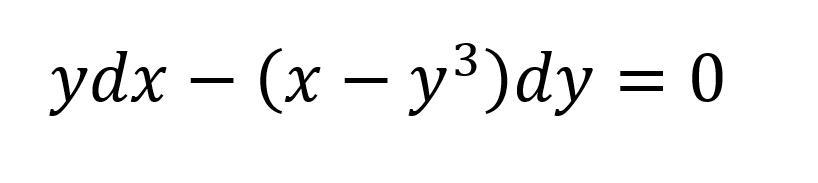
Ответы
Автор ответа:
0
Ответ:
Линейное диффер. уравнение 1 порядка относительно "х" .
Похожие вопросы
Предмет: Биология,
автор: fred1607
Предмет: Алгебра,
автор: SuperAndrey99
Предмет: Математика,
автор: gosha1290
Предмет: Биология,
автор: YARKarina
Предмет: ОБЖ,
автор: DianaTelukova