Question

Решите задачу по данным рисунка. Помогите пожалуйста очень надо

Answer 1

Ответ:  X=5

Решение:

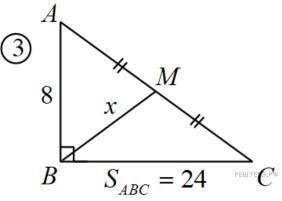
Дано: ΔАВС,∠ В=90°, АМ=МС, S(ABC)=24

Площадь прямоугольного треугольника равна половине произведения его катетов:

$S_{ABC}=\frac{1}{2}AB*BC;\\\\24=\frac{8*BC}{2};\\\\BC=24:4;\\\\BC=6$

По теореме Пифагора найдём АС:

$AC^2=BC^2+AB^2;\\AC=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10$

Это класический прямоугольный треугольник вокруг которого можно описать окружность с центром в точке М. Соответственно гипотенуза АС лежит на диаметре такой окружности и BM=АМ=МС=AC/2(  как радиус описаной окружности вокруг прямоугольного треугольника)

BM=10:2=5.

Если всё-таки нужно доказать, что BM=АМ=МС=AC/2 то найди в сети  тему прямоугольный треугольник, вписанный в окружность( там всё есть), но обычно учителя не требуют этих доказательств- достаточно знания про такую фишку:  медиана , проведённая из прямого угла к гипотенузе , является радиусом R описанной вокруг Δ окружности и равна половине гипотенузы.