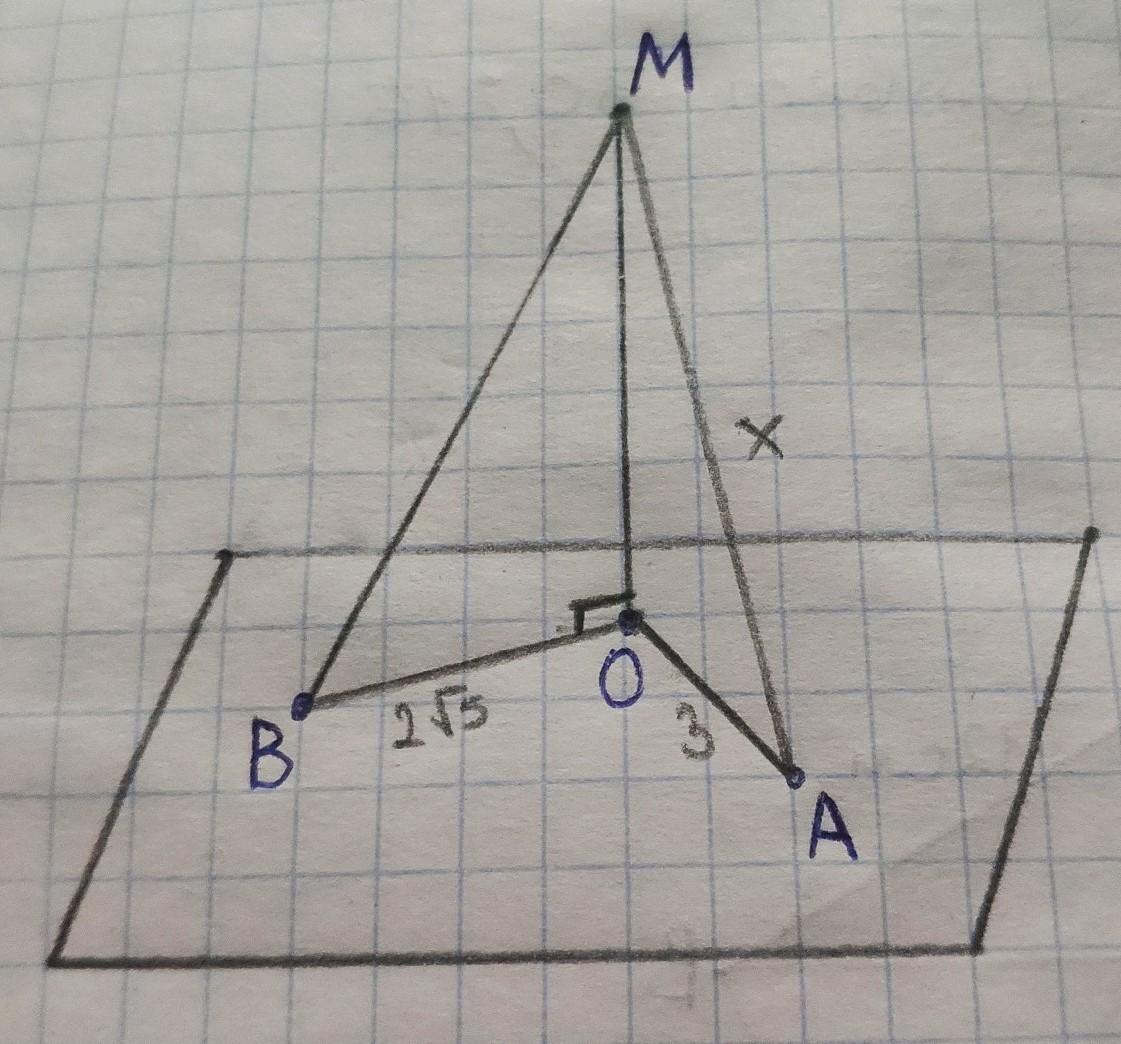
!!!З точки до площини проведено дві похилі, одна з яких на 1 см довша за другу.
Проекції похилих дорівнюють 2√5 см і 3 см. Знайдіть похилі.
(решение с рисунком)
Ответы
МА и МВ – наклонные, проведенные из точки М к плоскости. Проведём из точки М перпендикуляр МО к плоскости.
Отрезок соединяющий основание перпендикуляра и основание наклонной называется проекцией наклонной. Тогда АО – проекция МА, ОВ – проекция МВ.
Если прямая перпендикулярна плоскости, значит данная прямая перпендикулярна любой прямой, лежащей на этой плоскости. Следовательно угол МОА=90°, угол МОВ=90°, то есть треугольники МОА и МОА прямоугольные.
Пусть МА – меньшая наклонная и она будет равна х см, тогда МВ равна х+1 см, АО=3 см, ОВ=2√5 см.
В прямоугольном треугольнике МОА по теореме Пифагора:
МА²=МО²+АО²
МО²=МА²–АО²
МО²=х²–3² (Ур 1)
В прямоугольном треугольнике МОВ по теореме Пифагора:
МВ²=МО²+ОВ²
МО²=МВ²–ОВ²
МО²=(х+1)²–(2√5)² (Ур 2)
Поставим значение МО² из Ур 1 в Ур 2:
х²–3²=(х+1)²–(2√5)²
х²–9=х²+2х+1–20
х²–х²–2х=–20+1+9
–2х=–10
х=5
Тогда получим что МА=5 см, а МВ=6 см.
Ответ: 5 см, 6 см.