Предмет: Алгебра,
автор: magwan900
памагите плеаз я так больше не магу
Приложения:
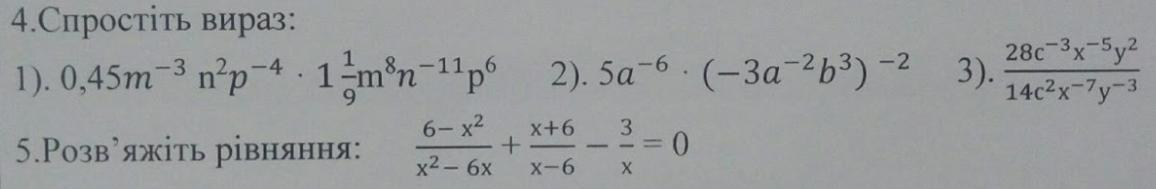
Ответы
Автор ответа:
0
4.
1)
2)
3)
.
5.
Приводим к общему знаменателю, который в данном случае равен .
Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. Тогда:
Приравниваем числитель к нулю, учитывая данное условие:
Ответ: -8.
Похожие вопросы
Предмет: Математика,
автор: gribkova98
Предмет: Математика,
автор: missg78
Предмет: Русский язык,
автор: kristi105
Предмет: Алгебра,
автор: tyfisa
Предмет: Математика,
автор: ariana350