Предмет: Алгебра,
автор: smith61
Найдите производную срочно! 75 баллов!
Приложения:
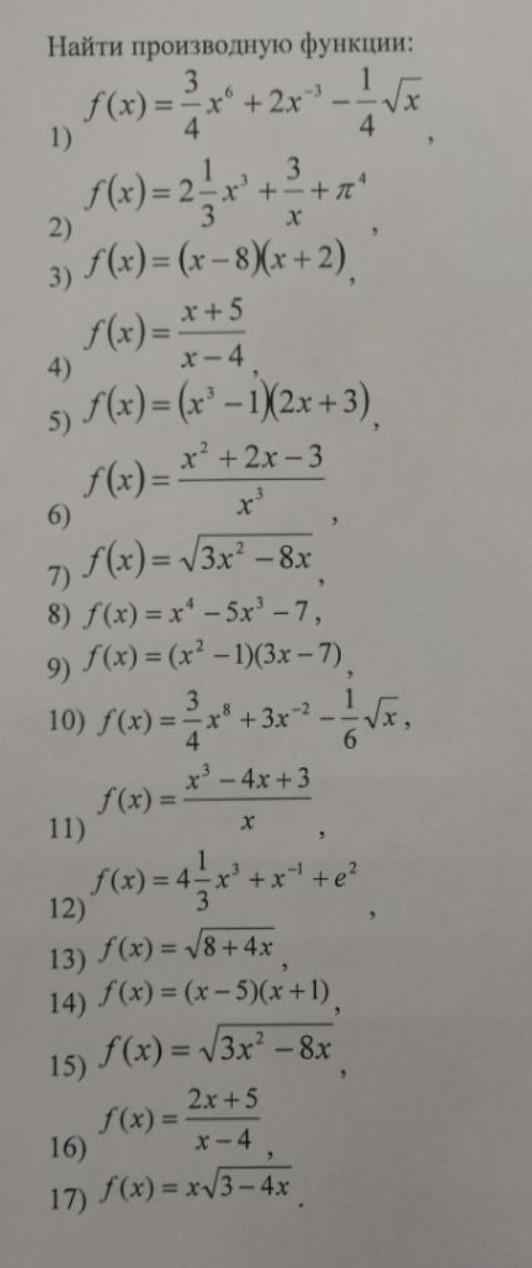
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Биология,
автор: galyagorlina
Предмет: История,
автор: vishcnia
Предмет: Математика,
автор: dlanochkashlsh
Предмет: Информатика,
автор: Ksusha22081
Предмет: Литература,
автор: Ирина20040812