Предмет: Геометрия,
автор: maksicprozukin
ПАЦАНЫ ООЧЕНЬ СРОЧНО ДАЮ 25 БАЛЛОВ
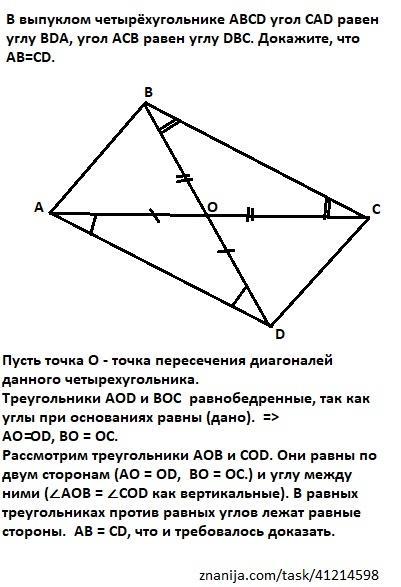
В выпуклом четырёхугольнике ABCD угол CAD равен углу BDA, угол ACB равен углу DBC. Докажите, что AB=CD. *
Ответы
Автор ответа:
2
Ответ:
Доказательство в объяснении.
Объяснение:
Пусть точка О - точка пересечения диагоналей данного четырехугольника. Треугольники AOD и ВОС равнобедренные, так как углы при основаниях равны (дано). =>
АО = OD и ВО = ОС.
Рассмотрим треугольники АОВ и СОD. Они равны по двум сторонам (АО = OD и ВО = ОС) и углу между ними (∠АОВ = ∠СОD как вертикальные). В равных треугольниках против равных углов лежат равные стороны. => АВ = CD, что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: fhfgkjfcghjfdghfjytr
Предмет: Русский язык,
автор: dalidaoo
Предмет: Русский язык,
автор: tuniklenchik
Предмет: Математика,
автор: jaz9
Предмет: Математика,
автор: svyznoi03