Предмет: Алгебра,
автор: Nurzhan94
Найдите f"(x) Вторая производная
Приложения:
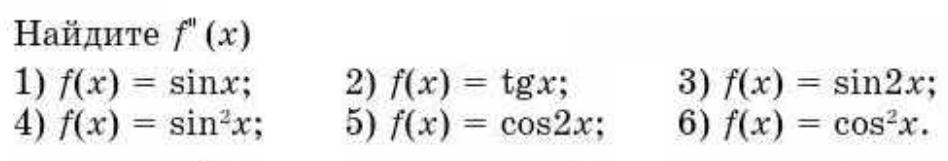
Ответы
Автор ответа:
0
Nurzhan94:
можно спросить если в тригонометрической задачи степень подставим вперед функции так, или как
y=sin^2(x). Степень переносится перед функцией, как и при дифференцировании обычной переменной в степени, только нужно нще взять производную от внутренней функции
у=sin^2(x) y'=2sin(x)*(sin(x))'=2sinx*cosx=sin2x
Похожие вопросы
Предмет: Русский язык,
автор: xyligan101
Предмет: Математика,
автор: epigida
Предмет: Английский язык,
автор: укропом11
Предмет: ОБЖ,
автор: lilsaturn
Предмет: История,
автор: lizavetazayka