Question

Серединный перпендикуляр биссектрисы AD треугольника ABC пересекает луч ВС в точке N. докажите что прямая NA-касательная к окружности, описанной около треугольника АВС.

Answer 1

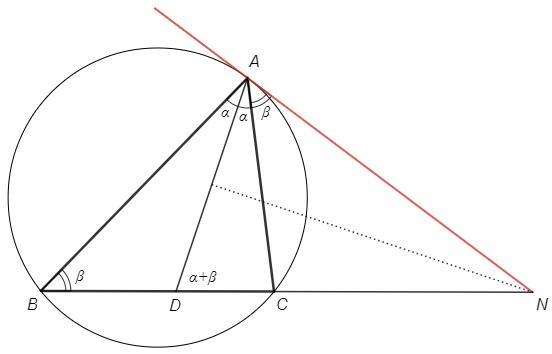
Точка N лежит на серединном перпендикуляре к AD, следовательно равноудалена от концов отрезка.

△AND - равнобедренный, DAN=ADN

DAN =A/2 +NAC

ADN =A/2 +B (внешний угол △BAD)

=> NAC =B =∪AC/2

Угол между прямой NA и хордой AC равен половине дуги, стягиваемой хордой, следовательно NA является касательной.

 

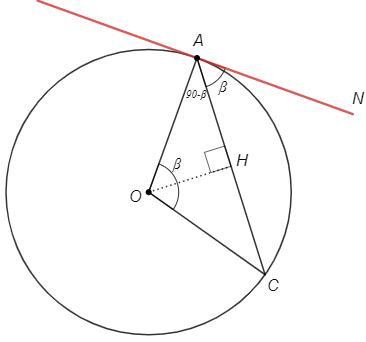
Докажем этот признак для острого угла NAC.

NAC =∪AC/2 =AOC/2 =AOH

△AOC - равнобедренный, OH - биссектриса и высота

OAH =90-AOH =90-NAC => OAN =OAH+NAC =90

Прямая NA перпендикулярна радиусу OA, следовательно является касательной.  

Для тупого угла как для смежного с NAC:

180-NAC =(360-∪AC)/2 => NAC=∪AC/2, далее по доказанному.