Предмет: Геометрия,
автор: Shapkina43
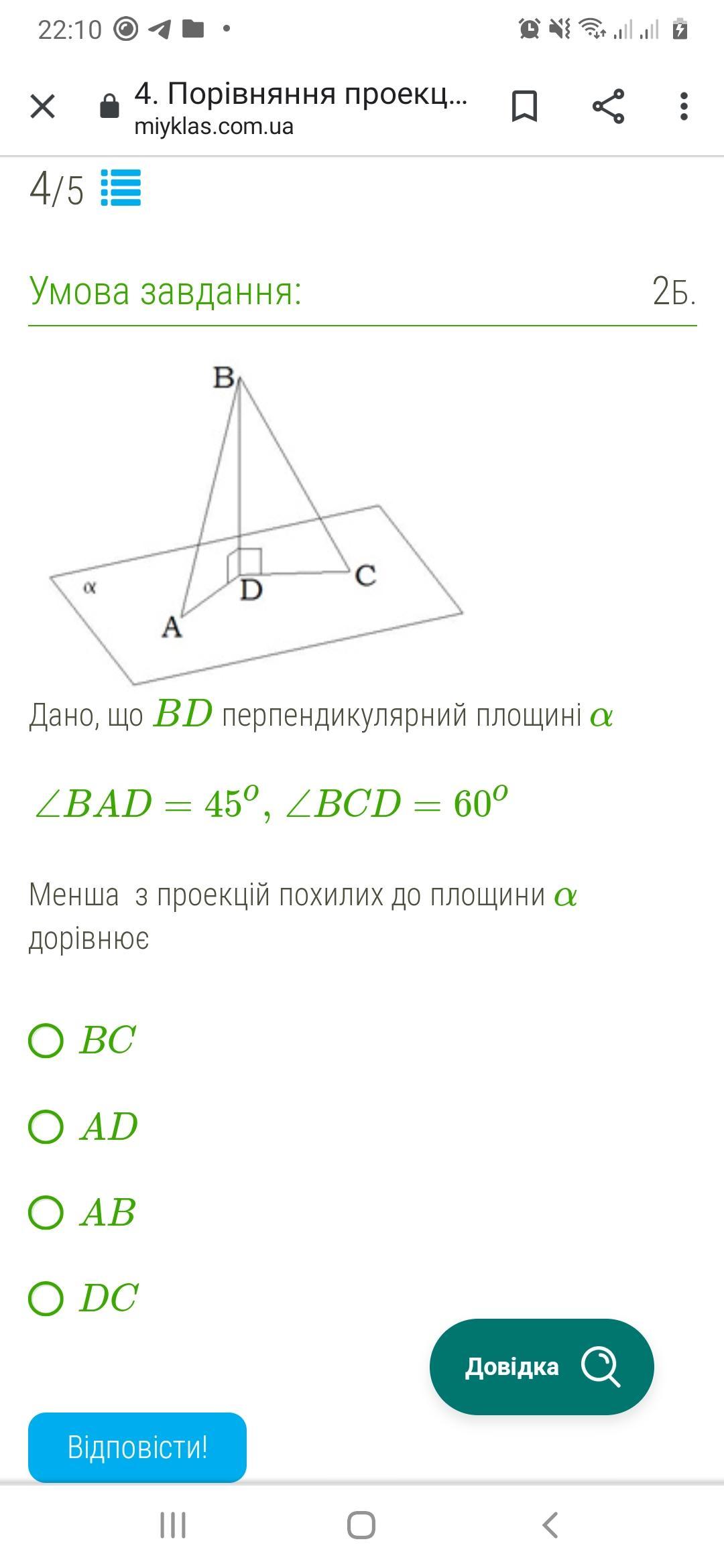
Дано, что BD перпендикулярен плоскости α
∠BAD = 45o, ∠BCD = 60o
Меньшая из проекций наклонных к плоскости α равна
Приложения:
Ответы
Автор ответа:
17
Ответ:
DC
Объяснение:
Так как BD⊥α ⇒ BD перпендикулярно любой прямой, принадлежащей плоскости α:
AD∈α, BD⊥α ⇒BD⊥AD
DС∈α, BD⊥α ⇒BD⊥DС
AB - наклонная к α, AD - её проекция.
ВС - наклонная к α, DС - её проекция.
ΔABD - прямоугольный. ∠D = 90°. Так как сумма углов треугольника равна 180°, то ∠АВD = 180-∠BDA-∠BAD=180-90-45=45°
ΔСBD - прямоугольный. ∠D = 90°.
∠СBD =180-∠BDC-∠BCD=180-90-60=30°
Так как напротив меньшего угла треугольника лежит меньшая сторона, то меньшая из проекций наклонных к плоскости α равна DC (∠СBD=30°, 30°<45°)
Похожие вопросы
Предмет: Математика,
автор: Rex2005
Предмет: Математика,
автор: stas200433
Предмет: Русский язык,
автор: kaleria2007
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: svetaelia