Question

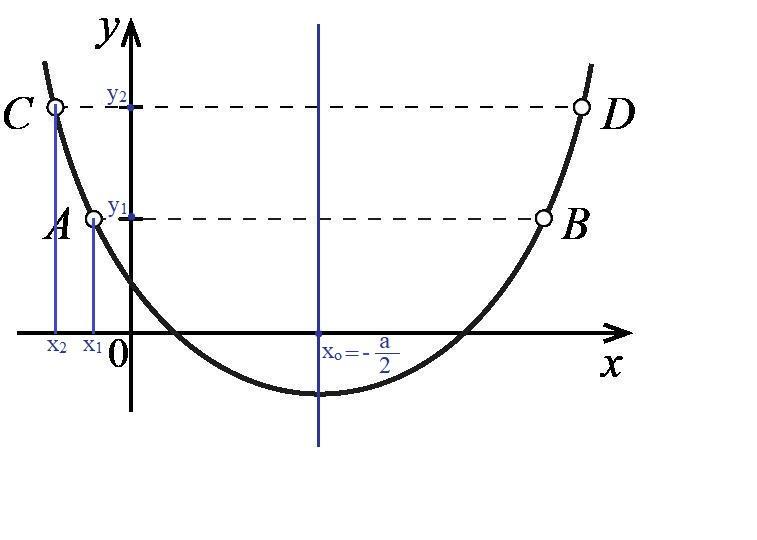
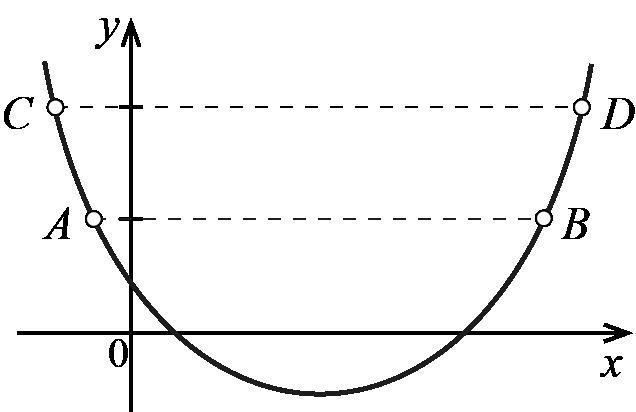
На рисунке дан график функции y=x^2+ax+b, AB||Ox, CD||Ox. Найдите расстояние между прямыми, если известно, что AB=3, CD=13. Народ пожалуйста, решите с четким объяснением, даю 40 баллов

Answer 1

Ответ:

Расстояние меду прямыми AB и CD равно 40 единиц.

Пошаговое объяснение:

1) Квадратичная функция задана формулой $\displaystyle y=x^{2} +ax+b.$

Найдем вершину параболы:   $\displaystyle x_{0} =-\frac{a}{2}$

Прямая, проходящая через вершину параболы параллельно оси Oy является осью симметрии параболы, эта прямая делит график на две равные части и делит отрезки AB и СD пополам.

2) Пусть точка A имеет координаты $\displaystyle (x_{1};\;y_{1})$, а точка C имеет координаты $\displaystyle (x_{2};\;y_{2})$.

Тогда расстояние вдоль оси Оx между точками x₁ и x₀ равно:

$\displaystyle x_{0}-x_{1}= \frac{AB}{2} =\frac{3}{2} =1,5; \Rightarrow x_{1}+1,5=x_{0}$

$\displaystyle x_{1}+1,5=-\frac{a}{2} ; \Rightarrow x_{1}=-\frac{a}{2} -1,5;$

расстояние вдоль оси Оx между точками x₂ и x₀ равно:

$\displaystyle x_{0}-x_{2}= \frac{CD}{2} =\frac{13}{2} =6,5; \Rightarrow x_{2}+6,5=x_{0}$

$\displaystyle x_{2}+6,5=-\frac{a}{2} ; \Rightarrow x_{2}=-\frac{a}{2} -6,5.$

Тогда

 $\displaystyle x_{1}+1,5=x_{2}+6,5;\\\\x_{1}-x_{2}=6,5-1,5=5.$

3) Расстояние между прямыми равно длине перпендикулярного отрезка, проведенного между этими прямыми.

В нашем случае расстояние между прямыми AB и CD равно расстоянию между координатами y₂ и y₁ вдоль оси Oy, то есть длине отрезка y₂ - y₁.

$\displaystyle y_{2}=x_{2} ^{2}+ax_{2}+b;\\\\y_{1}=x_{1} ^{2}+ax_{1}+b;$

$\displaystyle y_{2}-y_{1}=x_{2} ^{2}+ax_{2}+b-x_{1} ^{2}-ax_{1}-b=\\\\=x_{2}^{2}-x_{1}^{2}+ax_{2}-ax_{1}=(x_{2}-x_{1})(x_{2}+x_{1})+a(x_{2}-x_{1})=\\\\=(x_{2}-x_{1})(x_{2}+x_{1}+a).$

Если $\displaystyle x_{1}-x_{2}=5,$ то $\displaystyle x_{2}-x_{1}=-5.$

Оценим величину x₂ + x₁.

$\displaystyle x_{1}+x_{2}=-\frac{a}{2} -1,5-\frac{a}{2} -6,5=-8-a.$

Расстояние между прямыми:

$\displaystyle y_{2}-y_{1}=(x_{2}-x_{1})(x_{2}+x_{1}+a)=\\\\=-5 \cdot(-8-a+a)=-5 \cdot (-8) = 40.$