Предмет: Алгебра,
автор: XselloZ
дам 50 баллов! срочно! задание на фото
Приложения:
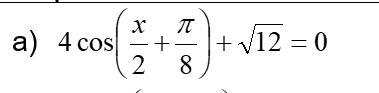
Ответы
Автор ответа:
1
Veronika724:
Тут тоже всё хорошо отображается?
да)
Похожие вопросы
Предмет: Химия,
автор: worums
Предмет: Русский язык,
автор: Настенька760
Предмет: Русский язык,
автор: artemmpalkin1
Предмет: Математика,
автор: 1УчениК11