Предмет: Геометрия, автор: tyreamina

Помогите пожалуйста
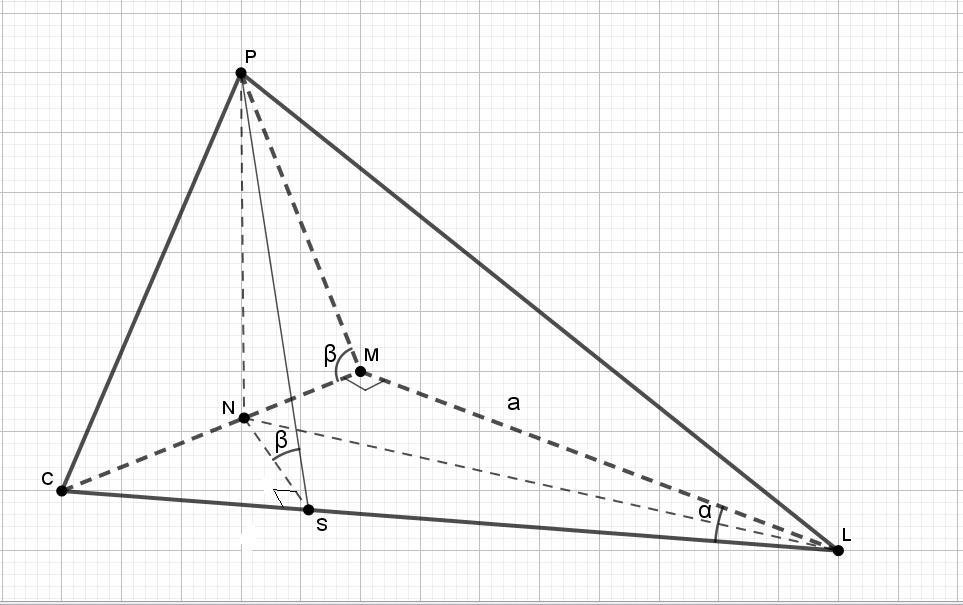
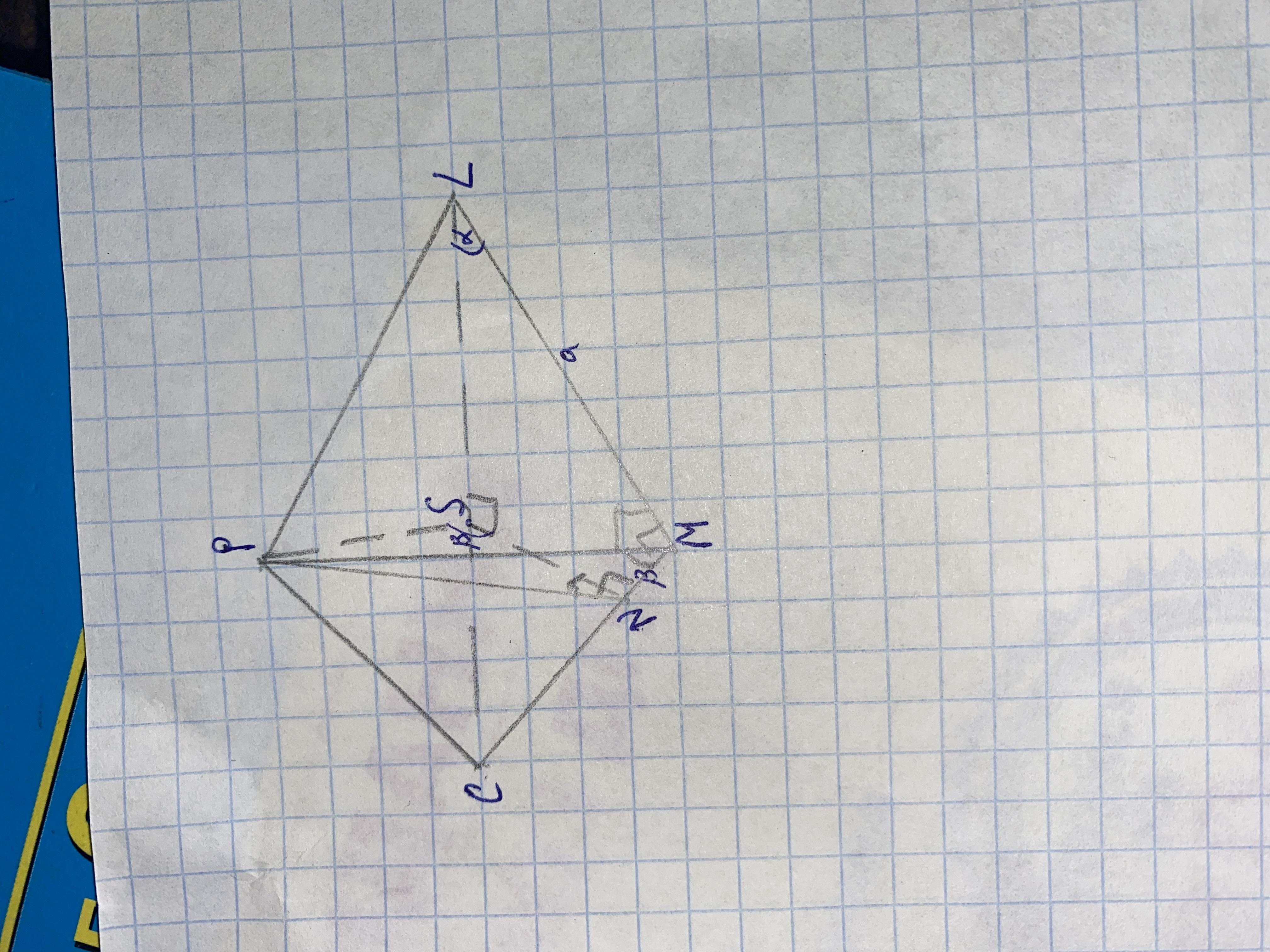
Найдите площадь боковой поверхности пирамиды, если известна сторона основы а, угол альфа и два угла бетта

Приложения:
dnepr1: Нужно более подробное изложение заданных условий. По рисунку не понятно - какой треугольник в основании (одного угла и одной стороны недостаточно для определения его параметров). Также - какие углы прямые?
dnepr1: Отрезок SN не может одновременно быть перпендикуляром к двум сторонам основания.
tyreamina: Основанием пирамиды является прямоугольный треугольник с катетом a и прилежащим к нему острым углом а. Боковая грань, содержащая другой катет этого треугольника,перпендикулярна к плоскости основания, а две другие-наклонены к плоскости основания под углом в.Определите боковую поверхность пирамиды.
dnepr1: Вот так и надо было давать задание!!!
dnepr1: В рисунок надо внести исправление - вместо SN надо 2 отрезка: OS и ON, где точка О - проекция высоты на основание.
dnepr1: Нет, не так. Так как грань МСР вертикальна, то верно: SN - отрезок, перпендикулярный к CL.

Ответы

Автор ответа: dnepr1
1

Так как две грани одинаково наклонены к основанию, то проекция ребра PL на основание - это биссектриса угла α.

Отрезок MN = a*tg(α/2).

Высота РН =  a*tg(α/2)/ tg(β).

Боковое ребро РМ - оно же и высота боковой грани PML - равно:

РМ = MN / cos(β) = a*tg(α/2)/cos(β).

Катет основания СМ =  a*tg(α).

Гипотенуза CL =  a/cos(α).

Высота PS грани CPL равна длине ребра РМ по равенству их проекций: MN = NS.

Теперь можно   определить площади боковых граней.

S(CPM) = (1/2)(a*tg(α))* a*tg(α/2)/ tg(β) =  (a²/2)*tg(α)*tg(α/2)/ tg(β).

S(PML) = (1/2)a*(a*tg(α/2)/cos(β)) =  (a²/2)*tg(α)*tg(α/2)/cos(β).

S(CPL) = (1/2)(a/cos(α))* (a*tg(α/2)/cos(β)) =  (a²/(2cos(α))*(tg(α/2)/cos(β)).

Осталось сложить:

Sбок = (a²/2)((tg(α/2)/tg(β))+ (tg(α/2)/cos(β)) + (tg(α/2)/(cos(α)*cos(β))).

Приложения:
ketebajcaat: ЗДРАВСТВУЙТЕ ДНЕПР МОЖЕТЕ ПОМОЧЬ ПО ГЕОМЕТРИИ, МОЕЙ ПРОФИЛЕ НА ВОПРОС?
Предыдущий вопрос
Следующий вопрос
Похожие вопросы
Предмет: Алгебра, автор: nargizoka2002
5x \frac{5x^{2} -5y ^{2}}{(5x-5y) ^{2} } <br />
1 год назад
Предмет: Математика, автор: AnNaVoRoZh
В летнем лагере 258 детей и 26 воспитателей. В автобус помещается 45 пассажиров. Сколько автобусов потребуется, чтобы всех перевезти из лагеря в город?
1 год назад
Предмет: Геометрия, автор: Лизачка1
в равнобедренном треугольнике АВС боковые стрроны АВ=ВС=5,медиана ВМ=4.Найдите cos угла ВАС???
1 год назад
Предмет: Математика, автор: Аноним
Остаток от деления числа 94 на 7 равен
1)3 2)4 3)5 4)6
8 лет назад
Предмет: МХК, автор: alina1427
срочно:)))
эссе "предсказания в искусстве" (не мало и не много)
8 лет назад