Предмет: Геометрия,
автор: bondarenkoelizaveta4
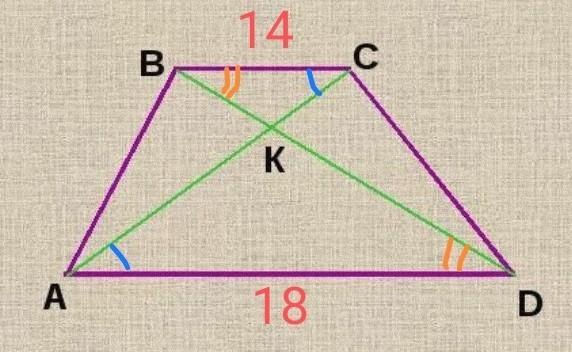
У трапеції ABCD (BC || AD) відомо, що AD = 18 см, ВС = 14 см,AC=24 см. Знайдіть відрізки, на які точка перетину діагоналей ділить діагональ АС?
Ответы
Автор ответа:
7
Ответ:
Диагональ АС делится на отрезки 13,5 и 10,5 см
Объяснение:
- ∆ADK ~ ∆BKC по 1 признаку:
∠KAD = ∠BCK как накрест лежащие при AD//BC и секущей АС;
∠KAD = ∠KBC как накрест лежащие при AD//BC и секущей BD
- Значит:
- АС = АК+КС => АК = АС - КС
- Теперь подставим:
Значит АК = 24-10,5 = 13,5 см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: sanua826
Предмет: Химия,
автор: natashasalamatk
Предмет: Русский язык,
автор: anarakerimova72
Предмет: Литература,
автор: ryabiets
Предмет: Математика,
автор: belaninaana809p0hpbu