Предмет: Геометрия,
автор: mordvintsevv
СРОЧНО Дано TRS RT= TS TE=8 RS=24 найти SK и TS
Приложения:
Ответы
Автор ответа:
2
Ответ:
2√85
Объяснение:
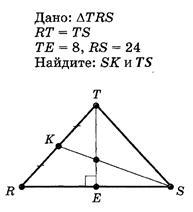
Дано: ΔTRS;
RT = TS;
TE = 8; RS = 24
Найти: SK и TS
Решение:
1. Рассмотрим ΔTRS.
RT = TS (условие)
⇒ ΔTRS - равнобедренный.
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
⇒ ТЕ - высота, медиана.
⇒ RE = ES = 24 : 2 = 12.
2. Рассмотрим ΔRTE - прямоугольный.
По теореме Пифагора найдем RT:
Тогда
3. Рассмотрим ΔRKS.
По теореме косинусов найдем KS:
⇒
Похожие вопросы
Предмет: История,
автор: alexrus319
Предмет: Математика,
автор: NikolKapral
Предмет: Английский язык,
автор: evgeniybazheno
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: EvaPark1997