Question

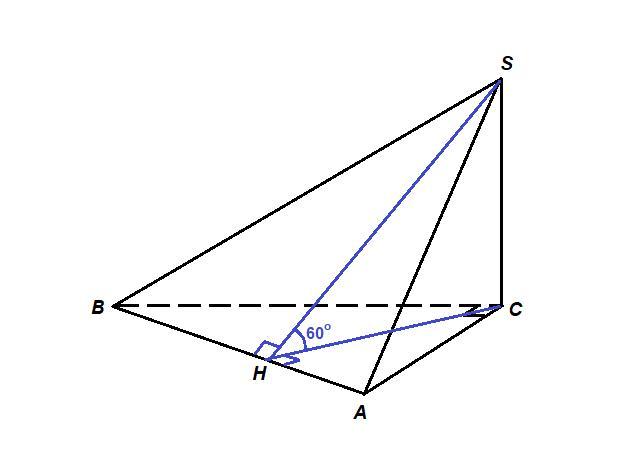
основанием пирамиды sabc является прямоугольный треугольник с прямым углом в вершине c. радиус окружности, описанной около этого треугольника равен 3 см. боковые грани acs bsc перпендикулряны плоскости основания пирамиды. грань abs наклонена к плоскости основания под углом 60 градусов, и ее площадь равна 12 корней из 2. найдите объем данной пирамиды
С рисунком и пояснениями.

Answer 1

Ответ:

8√3 см³

Пошаговое объяснение:

Дано: SABC - пирамида, ΔАВС: ∠С = 90°, R = 3 см,

(SAC)⊥(ABC), (SBC)⊥(ABC), ∠((SAB); (ABC)) = 60°

Ssab = 12√2 см²

Найти: V.

Решение:

Так как две пересекающиеся плоскости перпендикулярны основанию, то линия их пересечения - ребро SC - перпендикулярна основанию.

SC - высота пирамиды.

Проведем СН - высоту прямоугольного треугольника АВС.

СН - проекция SH на плоскость основания, значит SH⊥AB по теореме о трех перпендикулярах.  ⇒

∠SHC = 60° - линейный угол двугранного угла между плоскостью SAB и плоскостью основания.

Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы.

АВ = 2R = 2 · 3 = 6 см

Площадь ΔSAB:

$S_{SAB}=\dfrac{1}{2}AB\cdot SH$

$12\sqrt{2}=\dfrac{1}{2}\cdot 6\cdot SH$

$SH=\dfrac{12\sqrt{2}}{3}=4\sqrt{2}$  см

ΔSHC:  ∠SCH = 90°,

$SC=SH\cdot \sin\angle SHC=4\sqrt{2}\cdot \dfrac{\sqrt{3}}{2}=2\sqrt{6}$ см

$CH=SH\cdot \cos\angle SHC=4\sqrt{2}\cdot \dfrac{1}{2}=2\sqrt{2}$  см

Площадь основания:

$S_{ABC}=\dfrac{1}{2}AB\cdot CH=\dfrac{1}{2}\cdot 6\cdot 2\sqrt{2}=6\sqrt{2}$ см²

Объем пирамиды:

$V=\dfrac{1}{3}S_{ABC}\cdot SC$

$V=\dfrac{1}{3}\cdot 6\sqrt{2}\cdot 2\sqrt{6}=4\sqrt{2}\cdot \sqrt{6}=8\sqrt{3}$ см³