Question

В каком отношении делит площадь треугольника его сред­ няя линия?

помогите пожаста, даю 30 баллов

Answer 1

Ответ:

1 : 4

$\frac{S_{MBE}}{S_{ABC}} = \frac{1}{4}$

Объяснение:

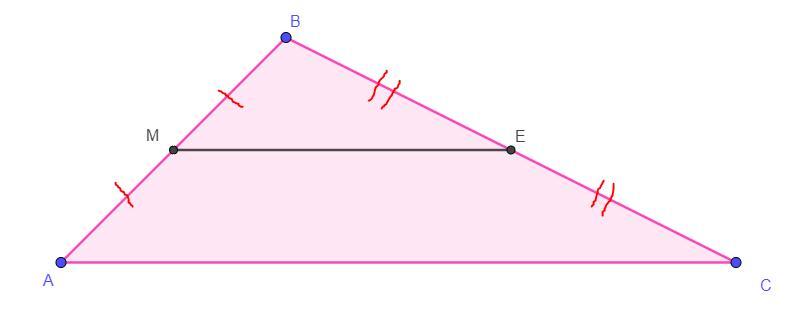
Дано: AM = MB, BE = CE, ME - средняя линия

Найти: $\frac{S_{MBE}}{S_{ABC}}$ - ?

Решение: Так как по условию AM = MB, BE = CE, то AB = AM + MB =

= MB + MB = 2MB, BC = CE + BE = BE + BE = 2BE. Треугольник ΔBME подобен треугольнику ABC, так как по свойству средней линии она делит треугольник на два подобных треугольников, тогда площади подобных треугольников соотносятся: $\frac{S_{ABC}}{S_{MBE}} = (\frac{AB}{MB} )^{2} \Longrightarrow S_{ABC} = S_{MBE} * (\frac{AB}{MB} )^{2} = BM * BE * 0,5 * \sin \angle ABC * (\frac{2MB}{MB})^{2} = 4 * BM * BE * 0,5 * \sin \angle ABC = 2 * BM * BE * \sin \angle ABC$

$\frac{S_{MBE}}{S_{ABC}} = \frac{0,5 * BM * BE * \sin \angle ABC}{2 * BM * BE * \sin \angle ABC} = \frac{0,5}{2} = \frac{5}{20} = \frac{1}{4}$