Question

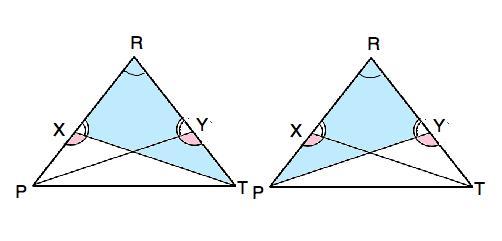
В треугольнике △PRT на стороне PR взяли точку X, а на стороне RT - точку Y так, что ∠PXT = ∠PYT, PY = TX.

Докажите, что RX = RY

Answer 1

 Сделаем рисунок и рассмотрим ∆ PRY и  ∆TRX.  Они имеют по два равных угла: ∠RXT=∠RYP как смежные данным по условию равным PXT=PYT, угол R - общий. Поэтому из суммы углов треугольника ∠RTX=∠ RPY.

В треугольниках  ∆ PRY и  ∆TRX  стороны PY = TX (дано), ⇒ они  равны по 2-му признаку равенства треугольников. ⇒

RX = RY, ч.т.д.