Предмет: Алгебра,
автор: Елизавета34501
Помогите, пожалуйста. Заранее спасибо.
Приложения:
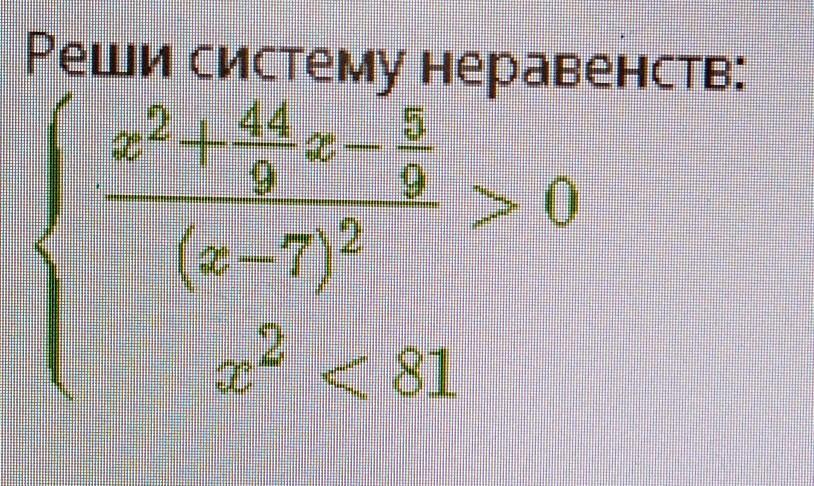
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: natasha0684
Предмет: История,
автор: Anastas2002
Предмет: Математика,
автор: adic123
Предмет: Математика,
автор: kot294
Предмет: Музыка,
автор: evgenstrashkov