Предмет: Математика,
автор: Geographist
Интеграл на фото! Знатоки помогите
Приложения:
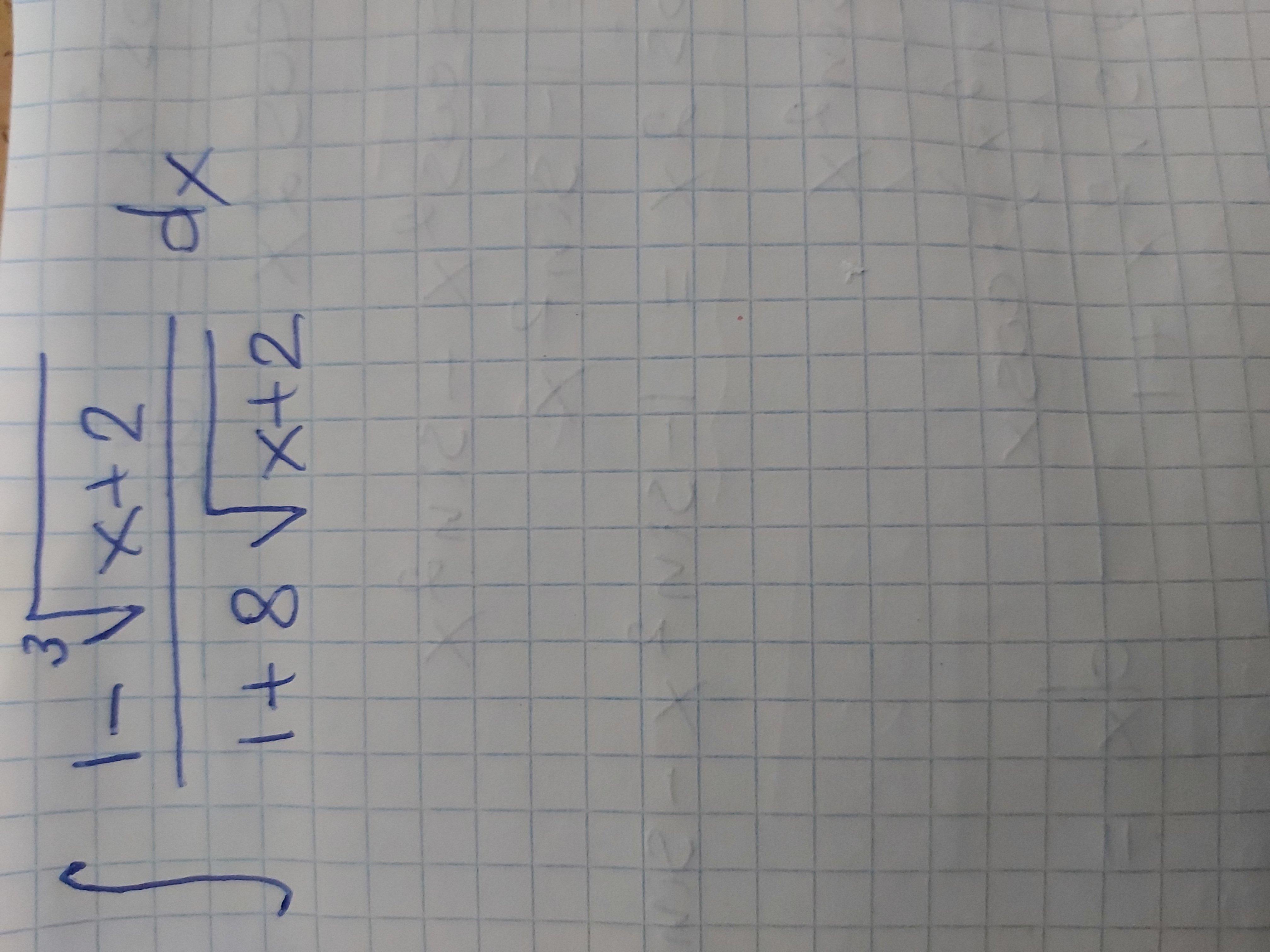
Ответы
Автор ответа:
1
Ответ:
Geographist:
Космос.. и этот интеграл был на ряду с простенькими.. зачем такое задавать...ужас
хороший интеграл, четыре метода интегрирования применяется и деление многочлена на многочлен ... есть и потруднее ...
Похожие вопросы
Предмет: Физика,
автор: Nastenk1997
Предмет: Русский язык,
автор: Суперпатрик2015
Предмет: Алгебра,
автор: Kleox
Предмет: Литература,
автор: Reshayka22811
Предмет: Математика,
автор: shermanakchurin