Question

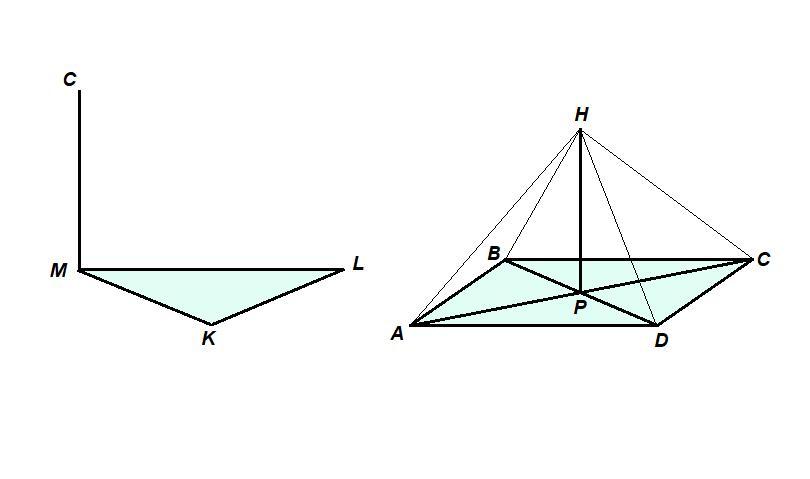
1. Прямая CM перпендикулярна плоскости треугольника

KLM. Докажите, что CM перпендикулярна прямой KL.

2. ABCD – квадрат, точка P – его центр.ПрямаяHP перпендикулярна к плоскости квадрата.

а) Докажите, что HA = HB = HC = HD.

б) Найдите HA, если AB = 8, PH = 2.
и рисунки

Answer 1

Ответ:

2. б) НА = 6

Объяснение:

1.

Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости.

СМ⊥(KLM), прямая KL лежит в плоскости (KLM), значит

СМ⊥KL.

2.

а) Диагонали квадрата равны и точкой пересечения делятся пополам, значит

РА = РВ = РС = PD.

Эти отрезки - проекции наклонных НА, НВ, НС и HD на плоскость (АВС).

Наклонные, проведенные из одной точки, равны, если равны их проекции, поэтому

НА = НВ = НС = HD.

б) АВ = 8, значит диагональ квадрата

АС = АВ√2 = 8√2

РА = 0,5 · АС = 0,5 · 8√2 = 4√2

Из прямоугольного треугольника НРА по теореме Пифагора:

НА = √(НР² + РА²) = √(4 + 32) = √36 = 6