Предмет: Математика,
автор: michaelmayers228
Решить одно дифференциальное уравнение. Помогите, пожалуйста, люди добрые.
Заранее спасибо

Приложения:
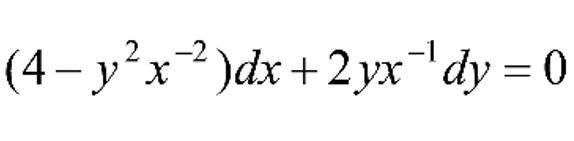
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Другие предметы,
автор: Faski
Предмет: Алгебра,
автор: 69Kosta69
Предмет: Математика,
автор: albu2002
Предмет: Математика,
автор: MarkT2007
Предмет: Математика,
автор: 111КАМИЛА111
505
https://znanija.com/task/41184706?utm_source=android&utm_medium=share&utm_campaign=question