Question

Для каждого из промежутков, изображеных на рисунке 7, укажите, содержаться ли в них точки:

(даю 100 балов)

Answer 1

Ответ и Объяснение:

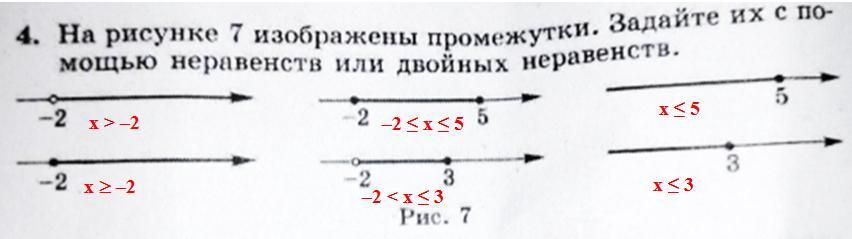
4. Промежутки задаются следующими неравенствами и двойными неравенствами (см. рисунок):

1) x > –2; 2) x ≥ –2; 3) –2 ≤ x ≤ 5; 4) –2 < x ≤ 3; 5) x ≤ 5; 6) x ≤ 3.

5. Даны точки:

а) 1;    б) –2;     в) $\dfrac{1}{6}$ ;    г) –3;    д) $3\dfrac{2}{7}$;    е) $-3\dfrac{4}{11}$.

Проверим, содержится ли точки в промежутках, заданных в 4.

1) x > –2:

а) х = 1 → 1 > –2 - верно, ДА;

б) х = –2 → –2 > –2 - неверно, НЕТ;

в) х = $\dfrac{1}{6}$ → $\dfrac{1}{6} >-2$ - верно, ДА;

г) х = –3 → –3 > –2 - неверно, НЕТ;

д) х = $3\dfrac{2}{7}$ → $3\dfrac{2}{7} >-2$ - верно, ДА;

е) х = $-3\dfrac{4}{11}$ → $-3\dfrac{4}{11} >-2$ - неверно, НЕТ.

2) x ≥ –2:

а) х = 1 → 1 > –2 - верно, ДА;

б) х = –2 → –2 ≥ –2 - верно, ДА;

в) х = $\dfrac{1}{6}$ → $\dfrac{1}{6} \geq -2$ - верно, ДА;

г) х = –3 → –3 ≥ –2 - неверно, НЕТ;

д) х = $3\dfrac{2}{7}$ → $3\dfrac{2}{7} \geq -2$ - верно, ДА;

е) х = $-3\dfrac{4}{11}$ → $-3\dfrac{4}{11} \geq -2$ - неверно, НЕТ.

3) –2 ≤ x ≤ 5:

а) х = 1 → –2 ≤ 1 ≤ 5 - верно, ДА;

б) х = –2 → –2 ≤ –2 ≤ 5 - верно, ДА;

в) х = $\dfrac{1}{6}$ → $-2 \leq \dfrac{1}{6} \leq 5$ - верно, ДА;

г) х = –3 → –2 ≤ –3 ≤ 5 - неверно, НЕТ;

д) х = $3\dfrac{2}{7}$ → $-2\leq 3\dfrac{2}{7} \leq 5$ - верно, ДА;

е) х = $-3\dfrac{4}{11}$ → $-2\leq -3\dfrac{4}{11} \leq 5$ - неверно, НЕТ.

4) –2 < x ≤ 3:

а) х = 1 → –2 ≤ 1 ≤ 3 - верно, ДА;

б) х = –2 → –2 < –2 ≤ 3 - неверно, НЕТ;

в) х = $\dfrac{1}{6}$ → $-2 < \dfrac{1}{6} \leq 3$ - верно, ДА;

г) х = –3 → –2 < –3 ≤ 3 - неверно, НЕТ;

д) х = $3\dfrac{2}{7}$ → $-2 < 3\dfrac{2}{7} \leq 3$ - неверно, НЕТ;

е) х = $-3\dfrac{4}{11}$ → $-2 < -3\dfrac{4}{11} \leq 3$ - неверно, НЕТ.

5) x ≤ 5:

а) х = 1 → 1 ≤ 5 - верно, ДА;

б) х = –2 → –2 ≤ 5 - верно, ДА;

в) х = $\dfrac{1}{6}$ → $\dfrac{1}{6} \leq 5$ - верно, ДА;

г) х = –3 → –3 ≤ 5 - верно, ДА;

д) х = $3\dfrac{2}{7}$ → $3\dfrac{2}{7} \leq 5$ - верно, ДА;

е) х = $-3\dfrac{4}{11}$ → $-3\dfrac{4}{11} \leq 5$ - верно, ДА.

6) x ≤ 3:

а) х = 1 → 1 ≤ 3 - верно, ДА;

б) х = –2 → –2 ≤ 3 - верно, ДА;

в) х = $\dfrac{1}{6}$ → $\dfrac{1}{6} \leq 3$ - верно, ДА;

г) х = –3 → –3 ≤ 3 - верно, ДА;

д) х = $3\dfrac{2}{7}$ → $3\dfrac{2}{7} \leq 3$ - неверно, НЕТ;

е) х = $-3\dfrac{4}{11}$ → $-3\dfrac{4}{11} \leq 3$ - верно, ДА.