В треугольнике АВС угол А = 45 градусов, АВ =8 корней из 2 и АС = 18. Координатным методом найдите медианы
Ответы
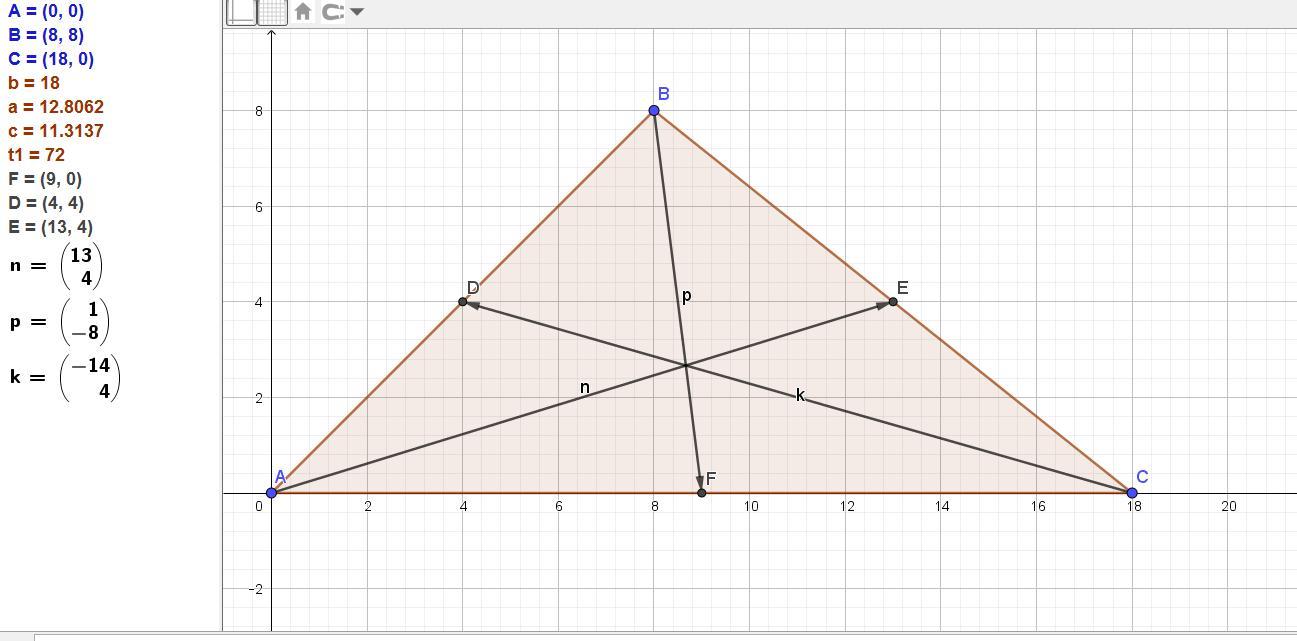
Дан треугольник АВС, угол А = 45 градусов, АВ =8 √2 и АС = 18.
Поместим его в прямоугольную систему координат точкой А в начало, точка В на оси Ох.
х(В) = AB*cos A = 8√2*(√2/2) = 8.
y(B) = AB*sin A = 8√2*(√2/2) = 8.
Получили координаты вершин.
А(0; 0), В(8; 8), С(18; 0).
Находим векторы сторон.
Координаты векторов
АВ ВС АС
х у х у х у
8 8 10 -8 18 0.
По свойству векторов медиана как половина диагонали параллелограмма на векторах сторон равна половине суммы векторов сторон.
Медианы
АА1 ВВ1 СС1
х у х у х у
13 4 1 -8 -14 4.
Модули (длины) медиан равны:
|AA1| = √(13² + 4²) = √(169 + 16) = √185 ≈ 13,60147.
|BB1| = √(1² + (-8)²) = √(1 + 64) = √65 ≈ 8,06226.
|CC1| = √((-14)² + 4²) = √(196 + 16) = √212 ≈ 14,56022.