Исследовать данную функцию на экстремум
z=(x-5)^2+y^2+1 (17 баллов, помогите)
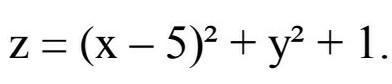
Ответы
Ответ: функция имеет минимум в точке М(5;0).
Пошаговое объяснение:
1 способ.
1) Находим первые и вторые частные производные:
dz/dx=2*(x-5), d²z/dx²=2, dz/dy=2*y, d²z/dy=2, d²z/(dxdy)=0.
2) Приравнивая первые частные производные к нулю, получаем систему уравнений:
2*(x-5)=0
2*y=0,
решая которую, находим координаты единственной критической точки М(5;0).
3) Обозначая теперь d²z/dx²(M)=2=A, d²z/(dxdy) (M)=0=B, d²z/dy²(M)=2=C, составим выражение A*C-B² и найдём его значение: A*C-B²=2*2-0=4>0, поэтому функция имеет экстремум в точке M. И так как при этом A>0, то это - минимум.
2 способ.
Так как (x-5)²≥0 и y²≥0, то z=(x-5)²+y²+1≥1. Отсюда следует, что данная функция имеет минимум при x-5=0 и y=0, т.е. при x=5 и y=0. А так как x и y могут принимать сколь угодно большие значения, то максимума функция не имеет.
z=tg|/xy (xy - под корнем)
https://znanija.com/task/41168661?utm_source=android&utm_medium=share&utm_campaign=question , пожалуйста